Spearman's Rank-Order Correlation for higher dimensions

Question

Spearman's Rank-Order Correlation Coefficient is a nonparametric measure of statistical dependence between two variables. It assesses how well the relationship between two variables can be described using a monotonic function.

So says Wikipedia.

My question: is it also possible extend this to higher dimensions?

Say I have scattered data of the form $(x_i,y_i,z_i)$, is it possible to compute Spearman's Rank-Order Correlation Coefficient to shed light on the question whether the relation between $x$ and $z$ can be described by a monotonic function?

I highlighted the word scattered, since I cannot simply fix $y$ and look upon it as data of the form $(x_i,z_i)$, because I only have a limited number of data, which is scattered.

Answer 1

Yes, you could in principle extend the idea of a rank correlation to higher dimensions as long as you have a way of ordering the points. For instance, consider two vectors $x_i = (x_{i1}, x_{i2}, \ldots , x_{ip})$ and $x_j = (x_{j1}, x_{j2}, \ldots, x_{jp})$. We could start by comparing the first two coordinates and say that $x_i < x_j$ if $x_{i1} < x_{j1}$ (or vice versa), and if $x_{i1} = x_{j1}$ then go to the next coordinate and repeat.

Now suppose we have a data set $\{ (x_1, y_1), (x_2, y_2), \ldots , (x_n, y_n) \}$ where each element is a pair of vectors. It's straightforward to apply an ordering such as the one above to the set of $x$ and $y$ vectors separately and convert each point to a pair of ranks and then calculate Spearman's rank correlation.

This shows that it's possible, but it's not clear when you would actually want to do this. In practice it would depend on whether or not some ordering makes sense and is interesting given the problem.

Answer 2

If you want to extend the idea of Spearman rank correlation to higher dimension and check for a comonotonic dependence between your $3$ variables, you can do the following:

1. Transform your data $X$, $Y$, and $Z$ with rank statistics into $ranks(X),ranks(Y),ranks(Z)$
2. If dependence is (perfectly) comonotonic, then the scatter plot must show a straight line; if it is imperfectly comonotic you will observe some dispersion from the diagonal.
3. To quantify the dependence, you can delve into copulas and find a way to measure the difference between perfect comonotic dependence (as expressed by the Frechet-Hoeffding upper bound copula) and the dependence you have measured. I have seen in the literature the use of $L_1$, $L_\infty$, optimal transport either on the copula density, or the cumulative distribution function.

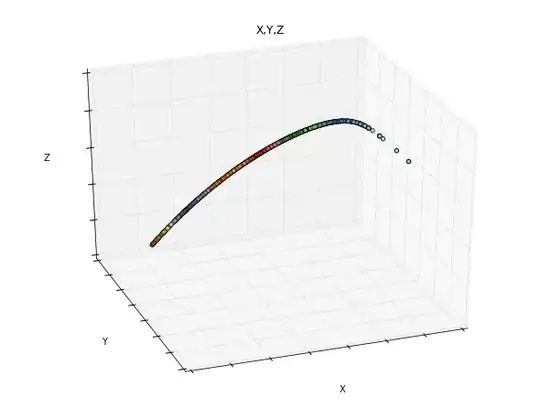
Scatter plot of the original data $X\sim \mathcal{U}[0,1], Y \sim \ln(X), Z \sim \exp(X)$

Scatter plot of the rank-transformed data (estimation of $F_X(X),F_Y(Y),F_Z(Z)$)

Example-code for producing the illustrations and doing the rank-transformation (empirical version of the probability integral transform):

import numpy as np
import scipy
from scipy import stats
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

n = 1000
X = np.random.uniform(0,1,n)
Y = np.log(X)
Z = np.exp(X)

#display the scatterplot of X,Y,Z
fig = plt.figure(1, figsize=(8, 6))
ax = Axes3D(fig, elev=-150, azim=110)
ax.scatter(X, Y, Z, c=X,
           cmap=plt.cm.Paired)
ax.set_title("X,Y,Z")
ax.set_xlabel("X")
ax.w_xaxis.set_ticklabels([])
ax.set_ylabel("Y")
ax.w_yaxis.set_ticklabels([])
ax.set_zlabel("Z")
ax.w_zaxis.set_ticklabels([])
plt.show()

#rank transform
Xrk = scipy.stats.rankdata(X)/n
Yrk = scipy.stats.rankdata(Y)/n
Zrk = scipy.stats.rankdata(Z)/n

#display the scatterplot of rank transform
fig = plt.figure(1, figsize=(8, 6))
ax = Axes3D(fig, elev=-150, azim=110)
ax.scatter(Xrk, Yrk, Zrk,c=Xrk,
           cmap=plt.cm.Paired)
ax.set_title("F_X(X),F_Y(Y),F_Z(Z)")
ax.set_xlabel("F_X(X)")
ax.w_xaxis.set_ticklabels([])
ax.set_ylabel("F_Y(Y)")
ax.w_yaxis.set_ticklabels([])
ax.set_zlabel("F_Z(Z)")
ax.w_zaxis.set_ticklabels([])
plt.show()

Answer 3

You might want to have a look at the following article: Taskinen, S., Randles, R., & Oja, H. (2005). Multivariate nonparametric tests of independence. Journal of the American Statistical Association, 100 (471), 916-925. It gives some (rather technical) generalisations of Spearman's rank correlation coefficient to higher dimensions in section 3.