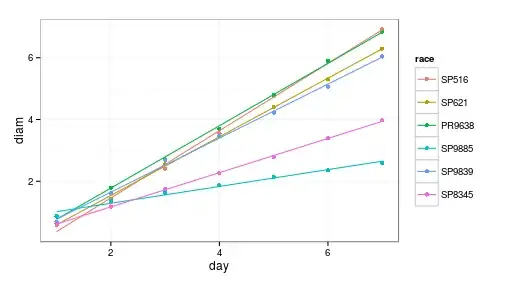
Testing Slope significance for multiple factor levels in a linear model

Question

I have 6 fungi races growing (diameter = diam [cm]) in Petri dishes.

zz <- "
day SP516   SP621   PR9638  SP9885  SP9839  SP8345
1   0.5825  0.6275  0.86    0.875   0.69    0.62
2   1.3425  1.44    1.79    1.3725  1.61    1.1825
3   2.4025  2.5525  2.715   1.6325  2.6925  1.7475
4   3.55    3.4625  3.69    1.87    3.46    2.2575
5   4.7725  4.4 4.79    2.135   4.225   2.7825
6   5.8975  5.3075  5.9075  2.3525  5.065   3.39
7   6.92    6.2925  6.8425  2.5975  6.04    3.975"

df <- read.table(text=zz, header = TRUE)

long = reshape2::melt(df, id.vars = "day",
            variable.name="race", value.name="diam") 

ggplot2::ggplot(long, aes(x = day, y = diam, color=race)) +  
    geom_point() + stat_smooth(method="lm", se=F)

I'd like to know if their growth rates are statistically different. How could I test it? the diameter at 0 day is 0.5 for all races, there the intercept could be forced to 0.5 cm.

Are these mean values? Or did you only measure 6 individual fungi strains over the period of one week? How many plates were there, how many measurements were done on individuals within plates? The problem is that, judging by your data, you don't really seem to have replicates per strain (only the same individual over time), do you? A bit more information would be helpful. — Stefan, Dec 23 '15 at 23:07
good point @Stefan, these are the mean values of 10 plates, assesed all of them every day. two measures were made in each plate... — Juanchi, Dec 24 '15 at 02:17
Can you tell me how many total observations did you have? 6 (strains) * 10 (plates) * 2 (each plate two individuals) * 7 (days) = 840 total observations? — Stefan, Dec 24 '15 at 02:46
mean value of two perpendicular measures in each plate containing one indivial fungus... which yields 6 (strains)* 10 (plates) * 1 (individual)* 7 (days) = 420 observations — Juanchi, Dec 24 '15 at 03:33
"growth rate" would normally suggest to me something in terms of *percentage* change from time period to time period. Are you definitely looking for a comparison of "change in diameter per day" across races (which would indeed be a slope comparison)? — Glen_b, Dec 26 '15 at 01:44

score 8 · Accepted Answer · answered Dec 23 '15 at 17:43

It depends on what you mean by statistically different. Statistically different from each other?

Looking at your plot, you've got four that look pretty clearly the same and then two that are much different. So, if you run:

library(lme4)
summary(lmer(diam~day*race + (1+day|race), data=long))

You get, in part:

Fixed effects:
               Estimate Std. Error t value
(Intercept)    -0.71786    0.11409  -6.292
day             1.08902    0.11022   9.880
raceSP621       0.36143    0.16135   2.240
racePR9638      0.48036    0.16135   2.977
raceSP9885      1.46143    0.16135   9.057
raceSP9839      0.61643    0.16135   3.820
raceSP8345      0.78071    0.16135   4.839
day:raceSP621  -0.13982    0.15588  -0.897
day:racePR9638 -0.07982    0.15588  -0.512
day:raceSP9885 -0.81652    0.15588  -5.238
day:raceSP9839 -0.21429    0.15588  -1.375
day:raceSP8345 -0.53491    0.15588  -3.432

lmer doesn't give p-values, because calculating degrees of freedom for these models isn't entirely straightforward, but looking at the t-value, you can see that you've got big values (in absolute terms) for the day:SP9885 interaction and the day:SP8345 interaction. This suggests that the slopes for those two conditions are shallower than the slopes for the others.

Technically, this is treating the SP516 group as the baseline, and testing everything else for differences from that.

If you wanted to set a different group as the baseline, you could run:

long$race <- relevel(long$race, ref='SP9885')
summary(lmer(diam~day*race + (1+day|race), data=long))

Truncated output:

Fixed effects:
               Estimate Std. Error t value
(Intercept)      0.7436     0.1176   6.324
day              0.2725     0.1086   2.508
raceSP516       -1.4614     0.1663  -8.789
raceSP621       -1.1000     0.1663  -6.615
racePR9638      -0.9811     0.1663  -5.900
raceSP9839      -0.8450     0.1663  -5.082
raceSP8345      -0.6807     0.1663  -4.094
day:raceSP516    0.8165     0.1536   5.314
day:raceSP621    0.6767     0.1536   4.404
day:racePR9638   0.7367     0.1536   4.795
day:raceSP9839   0.6022     0.1536   3.920
day:raceSP8345   0.2816     0.1536   1.833

If you're jonesin' for a p-value, you can see this faq

EDIT:

Using multilevel model here because I'm assuming that the observations across days are not independent for each of the fungi races. Thus, you've nested data.

Thanks @Triddle. Yes, I mean statistically different from each other. It seems that SP9885 and SP8345 are different from the rest, but what about between both of them? How could I test that? — Juanchi, Dec 23 '15 at 18:16
You relevel the factor to make one of them your baseline. That's what I did in the second version. The t-value for that comparison is 1.83. — triddle, Dec 23 '15 at 20:12
You can load the package `lmerTest` and re-run. That will give you p-values. In this case you will see that there are no degrees of freedom and the p-value is 1 for all fixed effects. So I would say you cannot test whether slopes are significantly different @Juanchi — Stefan, Dec 23 '15 at 20:37
You could do `lmer(diam ~ day + (1|race), long)` to assess diameter growth over time within races. — Stefan, Dec 23 '15 at 21:13

score 3 · Answer 2 · edited Apr 13 '17 at 12:44

3

Here's what I would do given the comments under your question:

## GENERATE SOME EXAMPLE DATA
set.seed(127)
d <- data.frame(
  plate = rep(c(1:10), 42, each = 2),
  strain = rep(c(letters[1:6]), 7, each = 20),
  day = rep(c(1:7), each = 120),
  diameter = rnorm(840, 6, 3)
  )

require(ggplot2) 
ggplot(d, aes(x = day, y = diameter)) + geom_point() + 
  geom_smooth(method = "lm") + facet_wrap(~strain)

require(lme4)
fit <- lmer(diameter ~ strain * day + (1|strain/plate), data = d)
summary(fit)

Don't forget to check the model fit with respect to the assumption of equal variances

plot(fit)
boxplot(residuals(fit) ~ d$strain + d$day)

To get an ANOVA table:

require(afex)
mixed(diameter ~ strain * day + (1|strain/plate), data = d, method='LRT')

The rest depends on which of your factors are significant. See here for a potential follow-up if your interaction is significant.

edited Apr 13 '17 at 12:44

Community

1

answered Dec 24 '15 at 16:07

Stefan

4,977
1
18
38

How would be the syntax model if I have this data factors (two experiment replicates): "experiment" "strain" "plate" "day" – Juanchi Jan 20 '16 at 14:11
@Juanchi I don't quite understand your question... – Stefan Jan 20 '16 at 20:20
I mean, how could I include the experiment factor in the model? – Juanchi Jan 20 '16 at 23:16
So you want know whether experiments are significantly different? Then just simply add `Experiment` to your fixed effects, i.e. `experiment * strain * day`, or `experiment + strain * day` if you are not interested in interactions of experiment with `strain` and `day`. If you did another experiment under the exact same condition for the sake of replication, you could also include it as a random effect `(1|experiment) + (1|strain/plate)`. But with only two levels it won't tell you much. – Stefan Jan 20 '16 at 23:27
Second option: it's a replicant of the first experiment under the same conditions... – Juanchi Jan 21 '16 at 01:19

jrp355 · Answer 3 · 2015-12-23T18:15:55.253

With multiple experimental replicates for each strain, you could use ANOVA to test if the slopes (growth rate) are statistically different. ANOVA will tell you if there are significant differences between the sample groups, not which strains are different. In order to do that you may want to use a multiple range test for comparing the means.

Edit:

You can preform linear regression for the growth of each strain to get the overall growth rate (the estimate for the day coefficient):

lm.SP516<-lm(df$SP516~df$day)
summary(lm.SP516)

Repeat for each strain, and storing the values in a vector "gr" (growth rate).

create vector with the names of the strains:

strain<-c(SP516,  SP621, PR9638, SP9885, SP9839, SP8345)

Carry out ANOVA:

dat<-data.frame(strain,gr)

fit<-aov(dat$gr~dat$strain))
summary(fit)

Given that the example data is repeatable, your answer would be much better if it included the code needed to implement it. — atiretoo, Dec 23 '15 at 17:43

score 0 · Answer 4 · answered Dec 23 '15 at 17:26

when you want to test whether the slope is different as a function of another variable, you include an interaction in the model. when the interacting variable is continuous, the slope changes linearly, but you can generalize this is a few ways. when the interacting variable is categorical, it allows different slopes in the different groups. see the wikipedia page

https://en.wikipedia.org/wiki/Interaction_(statistics)

for more info.

Testing Slope significance for multiple factor levels in a linear model

4 Answers4

Linked