0

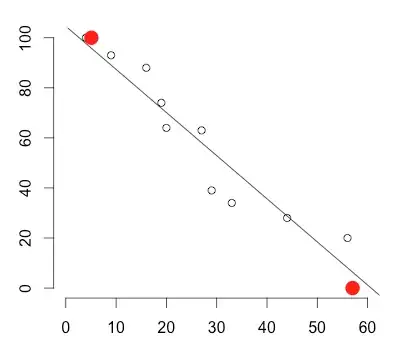
I'm dealing with a quantity that diminishes over time from 100% to 0%. I'm trying to plot the values, a lm abline, and large indicative points where the graph intersects y==100% and y==0%. I'm finding the results of lm(y~x) don't appear to be the inverse of lm(x~y) and I'm confused why this should be for a deterministic calculation. This illustrates in R:

set.seed(100)
d = data.frame(t = sort(sample(1:60,10)), q = sort(sample(1:100,10), dec=T))

# linear model - dependant y
fit = lm(q ~ t, d)

# predicting x where y == c(100,0) - i.e. dependant x
pred = predict.lm(lm(t ~ q, d), data.frame(q=c(100,0)), se.fit=T)$fit
pred = data.frame(t = pred, q = c(100,0))

plot.new()
plot.window(xlim=c(0,60), ylim=c(0,100))
axis(1); axis(2)
points(d)
abline(fit)
points(pred, pch=16, cex=2, col='red')

Why don't the red points not fall on the line? I know the modelling/plotting here is probably topsy-turvy, but I'm interested in the principal..

enter image description here

geotheory
  • 547
  • 2
  • 4
  • 14
  • you're right I think it is. I think I get why now. Still, that page could be a bit easier to find.. – geotheory Dec 09 '15 at 10:43
  • 1
    Agree, it took me few queries to find this thread even while knowing that it is somewhere there. But the community is one of the mechanisms behind this site ;) – Tim Dec 09 '15 at 10:47

0 Answers0