I only have a very basic understanding of statistics, but I want to see if the variables consonant, vowel, gender, speaker (as a random effect) have an effect on the Hertz of a vowel. So, Hertz is the dependent variable, and consonant, gender and vowel are the fixed effect. Speaker is a random effect.
I made this model in R:
lme(Hertz ~ consonant + gender + vowel, data = df, random =~ 1|speaker)
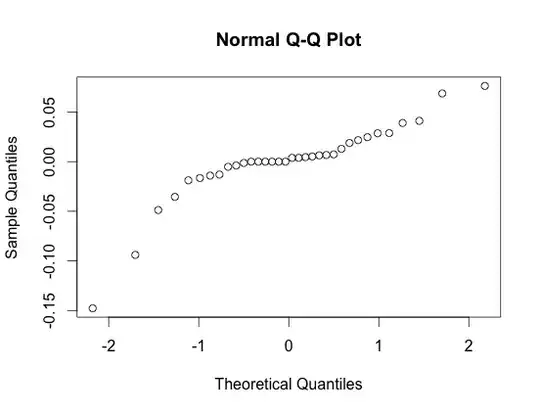
I made a quantile-quantile plot, but the results aren't linear. Do the residuals have to be linear? Here's the plot:
The main thing I want to do is see if the consonant has an effect on Hertz. Could I compare models to see if articulation has an effect? So, compare the log likelihood or AIC or BIC? Or maybe the residual plots? I don't know exactly what these mean, but I think they have something to do with being able to compare models.
lme(Hertz ~ gender + vowel, data = df, random =~ 1|speaker)