4

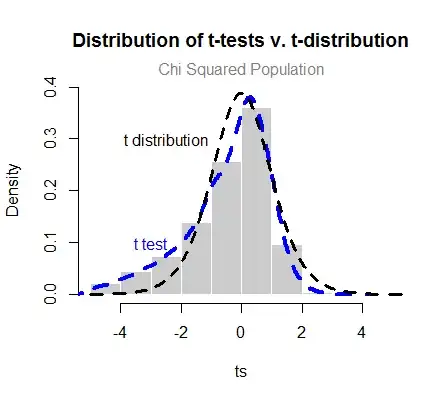
I am working through the concept of the need for normality in the underlying population when performing a t-test. This is nicely expounded by @Glen_b here. The gist of the explanation, I think, is that for the t test to follow a t distribution the numerator, $\bar X-\mu$, must be normally distributed, and also the denominator, $s\over \sqrt n$, is to fulfill the requirement that $s^2 \over \sigma^2$ conforms to a $\chi^2_d$, and be independent (numerator from denominator).

My questions are:

  1. Can it be shown with a Monte Carlo simulation (e.g., using R) that a t statistic on sample means extracted from a non-normal distribution doesn't necessarily follow a t distribution?
  2. What would be the repercussions of this for calculating confidence intervals along the lines of the discussion here. Jotting down a likely explanation would be that the issues that apply to the application of a t-test to compare sample means (discussed on the first hyperlinked post) are simply not applicable to sampling distributions as a result of the CLT.

As a way of example of what I'm considering, a possible (probably flawed) approach to the first part of the question would be to extract samples from a $\chi^2_1$. Thanks to the help from the commenters at this point I got this plot with code here:

enter image description here

This is surprising because I expected to see more of a discrepancy between the t-statistic and the t-test based on the underlying population (chi-squared). Although perhaps it should not be surprising at all if we compare it with samples from the almighty Normal, which fit just so:

enter image description here

So is the offset in the first plot "clearly" off? Is it fair to compare it to the normal? Just side questions, the actual points I am asking are clearly stated above.

EDIT: If there is no official answer, I want to at least reflect here the valuable tip offered by @Scortchi in the comments to illustrate how real the offset is:

The 0.5% quantile for the t-test statatics generated in the simulation quantile(ts, 0.005) = -9.682655, whereas qt(0.005, df=9) = -3.249836.

Community
  • 1
Antoni Parellada
  • 23,430
  • 15
  • 100
  • 197
  • 1
    You also need independence of the numerator and denominator. If the values are iid normal, you should have all three at once. However, "*I wanted to see this in a simulation*" needs to be rephrased to be in the form of a question, since it's not especially clear what you seek. What is it you want to know? – Glen_b Nov 30 '15 at 11:59
  • You're welcome, @AntoniParellada. This is my interpretation of what your implicit questions were. Feel free to re-edit to ensure that it matches your intent as closely as possible. – gung - Reinstate Monica Nov 30 '15 at 17:20
  • 3
    The line computing `ts` does not make sense to me. You should be computing t-statistic for each of your 1000 samples by dividing that sample's mean (with null hypothesis value subtracted) by *that sample's* standard error of the mean. – amoeba Nov 30 '15 at 17:34
  • Make a function to simulate the $n$ chi-squared r.v.s & calculate the t-statistic to test the null hypothesis that the true mean is one (which it is for a chi-squared r.v. with 1 df): `t.stat.sim – Scortchi - Reinstate Monica Nov 30 '15 at 17:39
  • @Scortchi I kind of blended your suggestion with my original code and amoeba's comment, but the result seems to actually prove the opposite of what I intended. [Here's "my" new simulation](https://github.com/RInterested/Scrapbook/blob/master/t%20statistic). – Antoni Parellada Nov 30 '15 at 18:35
  • 1
    (1) As a check of your code, consider running it for samples from a Normal distribution to ensure that you *do* obtain a t-distributed result. (2) You might find the thread at http://stats.stackexchange.com/questions/69898 to be of some relevance. I think its analysis goes beyond the limited discussion in the (old) thread you reference in (2). Note the [comment](http://stats.stackexchange.com/questions/69898/t-test-on-highly-skewed-data#comment346545_69967) by @glen_b. – whuber Nov 30 '15 at 19:02
  • @whuber Thanks about the tip on running the code on normal data. Right now the problem I'm having (after incorporating Scortchi and amoeba comments, is that the t-test seems to actually follow the t-distribution in samples from chi squared (1df) as [in here](https://github.com/RInterested/Scrapbook/blob/master/t%20statistic). – Antoni Parellada Nov 30 '15 at 20:07
  • Hmmm... it better not do that. If it is, there is an error in your code. – whuber Nov 30 '15 at 20:15
  • @whuber I used the deleted "Answer" to show you. – Antoni Parellada Nov 30 '15 at 20:21
  • Doesn't seem all that close. Compare some quantiles in the tails of the simulated t statistic `quantile(ts, c(0.005, 0.025, 0.05)` with those of Student's t distribution `qt(0.025, df=9)`. It's these you'd use in forming tests & confidence intervals. Often it's useful to plot cumulative distribution functions & zoom in on the tails. – Scortchi - Reinstate Monica Dec 01 '15 at 10:22
  • @Scortchi Thank you very much for your help. On the first expression, `ts` is as defined in your prior comment, or in the code that I share on a hyperlink, and that I used to generated the plots? And, on the second expression, I can't find `sample_ts` defined on either your code or mine. – Antoni Parellada Dec 01 '15 at 13:52
  • Sorry, corrected. `ts` as in your code (should be the same anyway) but without the truncation `ts -5]` (which I don't understand). – Scortchi - Reinstate Monica Dec 01 '15 at 13:57
  • @Scortchi And `sample_ts`? – Antoni Parellada Dec 01 '15 at 13:59
  • Ignore: I ran a bit of your code & started to call `ts` that by mistake, then copied it instead of `qt(0.975, df=9)`. I edited the code in the comment above. – Scortchi - Reinstate Monica Dec 01 '15 at 14:09
  • 1
    You mean `qt(0.005, df = 9)` instead of `qt(0.975, df=9)`, correct? – Antoni Parellada Dec 01 '15 at 14:13
  • @AntoniParellada: Yes, sorry. Changed that now too. – Scortchi - Reinstate Monica Dec 04 '15 at 12:15
  • @Scortchi Thank you!!! I'm overwhelmed sorting through the answers to this question :-D No, really, my Bayesian probability of getting an answer here is zero. So could you be your usual kind self and tell me if my implicit answer in the question is now correct? – Antoni Parellada Dec 04 '15 at 14:33
  • @AntoniParellada: The simulation seems fine (Q1). As for Q2, you've not developed it much. – Scortchi - Reinstate Monica Dec 04 '15 at 14:40
  • @Scortchi Thanks again. Correct. I did edit the question at some point, though, hinting at a possible answer: The CLT makes it OK to apply the *t* to calculate confidence intervals regardless of the normality of the underlying distribution. For comparison of means between groups, on the other hand, we need to make sure that the underlying population is normal. – Antoni Parellada Dec 04 '15 at 14:44
  • I don't understand why you're making that distinction. The goodness of the approximation of the distribution of the t statistic to Student's t distribution is what justifies its use in both confidence intervals around for the true meas (or a difference in true means) & tests that the true mean (or a difference in means) is some particular value. (You might expand your simulation to include calculation of confidence interval bounds & p-values for tests. That the approximation gets worse further out in the tails suggests a 99% confidence interval will be less reliable than a 95% one, & ... – Scortchi - Reinstate Monica Dec 04 '15 at 14:56
  • I just don't know how to formulate the question to get a response - it seems as though we calculated CI's for everything under the sun using *t* intervals without much thought about normality; yet, when it comes to comparing means between groups the concerned reflected in this very same post and in the [superb post by Glen_b](http://stats.stackexchange.com/a/152266/67822) about normality of the underlying population becomes a true concern. You've done more than enough trying to help, though, and I'm just explaining where I'm stuck. – Antoni Parellada Dec 04 '15 at 15:14
  • ... a critical value for a test with a significance level of 1% less reliable than one for a test with a significance level of 5%.) – Scortchi - Reinstate Monica Dec 04 '15 at 15:14
  • @Scortchi sorry, I didn't see you're edit to the comment until I had already posted... – Antoni Parellada Dec 04 '15 at 15:16
  • 1
    @Glen_b's points are (I think) that (1) the t statistic only follows Student's t distribution *exactly* when the data are from a normal distribution, & (2) you don't know *how closely* it'll follow it in small-to-moderate size samples - it depends on how close the data's distribution is to a normal distribution. Your simulation answers the latter question for a particular case. – Scortchi - Reinstate Monica Dec 04 '15 at 15:36

0 Answers0