Can any sort of conclusion be made about the cointegration of $B, A$ given the cointegration test statistic of $A, B$?

Question

It can be shown that, generally, the cointegration test statistic of $A, B \ne B,A$. I believe this to be true for all cointegration tests, so the particular test used is, perhaps, irrelevant.

However, I have found that the two test statistics are generally "close": the two test statistics will be in the same confidence level.

Note that in my work the common method to test for cointegration is to test for a unit root in the linear combination of the two series (AKA residual series). Generally I will do so by using the ADF test and compare the resulting test statistic to the confidence levels required to reject the null hypothesis.

My questions:

1. Are there any formal things that can be said about the comparison of $coint(A,B)$ to $coint(B,A)$?
2. Is there a compelling technical reason to prefer one variable orientation over the other?
3. Are the answers to 1 or 2 particular to the cointegration test used? If so, is there anything particularly relevant to the cointegration test methodology I outlined above?

Thanks.

EDIT:

Here's an example, as requested. I use Python for most of my statistical work.

The ADF test statistic for the first linear combination (AKA residual series) is -35.9199966497 and -35.7190914946 for the second linear combination.

Obviously this is a rather extreme example, but there are many others.

Order of plots in the graph:

1. Residual series 1
2. Scatter plot with line of best fit, (x,y) orientation.
3. Residual series 2
4. Scatter plot with line of best fit, (y,x) orientation.
5. Graph of the two raw curves.

Hopefully that clears things up.

Answer 1

For two time series $X_t$ and $Y_t$ to be cointegrated two conditions are met:

1. $X_t$ and $Y_t$ must be $I(1)$ processes, i.e. $\Delta X_t$ and $\Delta Y_t$ must be stationary processes (in a weak sense, i.e. covariance stationary).

2. There exists a set of coefficients $\alpha,\beta\in \mathbb{R}$ such that the time series $Z_t=\alpha X_t+\beta Y_t$ is a stationary process. The vector $(\alpha,\beta)$ is called cointegrating vector.

Since stationarity is invariant to shift and scale it immediately follows that coefficients $\alpha$ and $\beta$ are not uniquely defined, namely they are unique up to multiplicative constant.

Cointegration tests come in two varieties:

1. Tests on residuals of regression of $Y_t$ on $X_t$.

2. Tests on matrix rank in a vector-error correction representation of $(Y_t,X_t)$.

Both varieties rely on certain theoretical results, namely:

1. OLS of $Y_t$ on $X_t$ gives a consistent estimate of cointegration vector

2. Granger representation theorem.

The OP question is about the first variety of tests. In these tests we have a choice: estimate regression $Y_t=a_1+b_1 X_t+u_t$ or $X_t=a_2+b_2 Y_t+v_t$ on $Y_t$. Naturally these two regressions will give two different cointegrating vectors: $(-\hat b_1, 1) $ and $(1, -\hat b_2)$. But due to above mentioned theoretical result the probability limits of $-\hat b_1$ and $-1/\hat b_2$ must be the same, since the cointegrating vector is unique up to a constant.

Due to algebraic properties of OLS the residual series $\hat u_t$ and $\hat v_t$ are not identical, although from theoretical perspective they both should be equal to $\frac{1}{\beta}Z_t$ and $\frac{1}{\alpha}Z_t$ respectively, i.e. they should be identical to multiplicative constant. If the series $X_t$ and $Y_t$ are cointegrated then $Z_t$ is a stationary series, so since $\hat u_t$ and $\hat v_t$ approximate $Z_t$ we can test whether they are stationary.

That is how the first variety of cointegration tests are performed. Naturally since the $\hat u_t$ and $\hat v_t$ are different any tests on them will differ too. But from theoretical point of view any difference is simply a finite sample bias, which should disappear asymptotically.

If the difference between the stationarity tests on series $\hat u_t$ and $\hat v_t$ is statistically significant, this is an indication that the series are not cointegrated, or assumptions of stationarity tests are not met.

If we take ADF test as a stationarity test for residuals I think it would be possible to derive asymptotic distribution of difference between the ADF statistics on $\hat u_t$ and $\hat v_t$. Whether it would have any practical value I do not know.

So to summarize the answers to the three questions are the following:

1. See above.

2. No.

3. The asymptotic distribution of difference of the tests would depend on the test. Your methodology is fine. If time series are cointegrated, both statistics should indicate so. In case of no cointegration, either both statistics will reject stationarity, or one of them will. In both cases you should reject the null hypothesis of cointegration. As in testing for unit root you should safeguard against time trends, change points and all the other things that make unit root testing quite challenging procedure.

Answer 2

So the most popular answer of statistics is apparently correct for this question: "it depends".

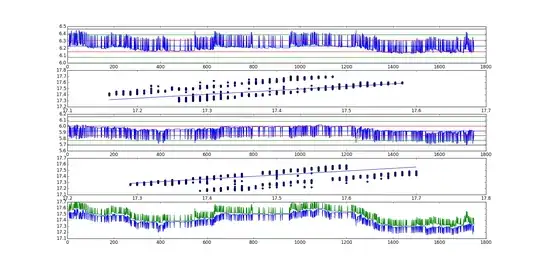
A good guess can be made about the similarity of cointegration test statistics of unique orderings of input variables, given that the time series vectors have low and similar variances.

This is implied from the calculation of the cointegration test statistic: when the variances of the input time series vectors are low and similar, the cointegration coefficients will be similar (which is to say, approximately scalar multiples of each other), resulting in the residual series being approximately scalar multiples of each other. Similar residual series implies similar cointegration test statistics. However, when the variances are large or dissimilar, there is no implied guarantee that the residual series will be even approximately scalar multiples of each other, which in turn makes the cointegration test statistics variable.

Formally:

Consider the simple regression model, used to find the cointegration coefficient for bivariate cases.

Regressing x on y: $$ \hat{\beta}_{xy} = {Cov[x,y] \over \sigma_x^2 } $$

Regressing y on x: $$ \hat{\beta}_{yx} = {Cov[y,x] \over \sigma_y^2 } $$

Clearly $Cov[x,y] = Cov[y,x]$.

But, generally, $ \sigma^2_x \neq \sigma^2_y $.

Thus, $ \hat{\beta}_{xy} $ is not a scalar multiple of $ \hat{\beta}_{yx} $.

So the linear combinations (AKA residual series) that are used to test for a unit root to determine likelihood of cointegration are not scalar multiples of one another: $$ x_t - \gamma^1 y_t = \epsilon_t^1 $$ $$ y_t - \gamma^2 x_t = \epsilon_t^2 $$

Note that, therefore, $ \gamma = \hat{\beta} $, so generally $ \gamma^1 \neq a*\gamma^2 $ for some scalar $a$.

This shows two facts about cointegration:

1. The variable order in testing for cointegration matters because of the variance of the individual time series vectors. This affects the relationship between the cointegration coefficients of the various variable orientations because of how the cointegration coefficient is calculated.
2. The residual series may or may not be "similar" to one another: the similarity depends on the variances of the individual time series vectors.

These facts imply that the residual series formed by unique variable orderings are not only different, but they are probably not scalar multiples of one another.

So which ordering to choose? It depends on the application.

Why do some residual series as generated from the same data series but different orderings appear similar while others appear so different? It is because of the variance of the individual time series vectors. When the time series vectors have similar variance (as is certainly possible when comparing similar time series data), the residual series may seem like $-1 * \alpha$ multiples of one another, with $\alpha$ being some scalar value. This is the case when the variance of the time series vectors are both low and similar, resulting in similar error terms in the linear combinations.

So, finally, if the time series vectors that are being tested for cointegration have low and similar variances, then one can correctly suppose that the cointegration test statistic will be of a similar confidence level. In general, it is probably best to test both orientations, or at least consider the variances of the time series vectors, unless there is a prevailing reason to favor one orientation.