How to kernelize a simple perceptron?

Question

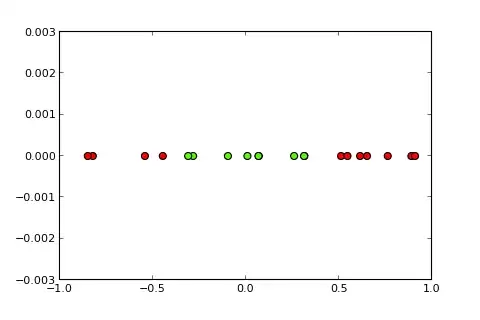
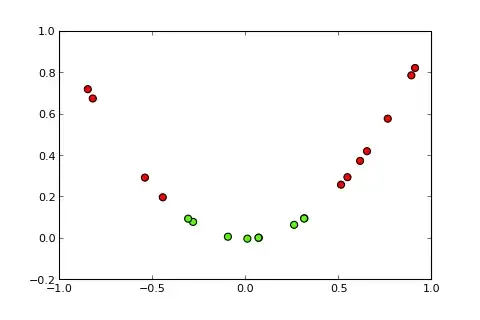
Classification problems with nonlinear boundaries cannot be solved by a simple perceptron. The following R code is for illustrative purposes and is based on this example in Python):

nonlin <- function(x, deriv = F) {
  if (deriv) x*(1-x)
  else 1/(1+exp(-x))
}

X <- matrix(c(-3,1,
              -2,1,
              -1,1,
               0,1,
               1,1,
               2,1,
               3,1), ncol=2, byrow=T)

y <- c(0,0,1,1,1,0,0)

syn0 <- runif(2,-1,1)

for (iter in 1:100000) {
  l1 <- nonlin(X %*% syn0)
  l1_error <- y - l1
  l1_delta <- l1_error * nonlin(l1,T)
  syn0 <- syn0 + t(X) %*% l1_delta
}

print("Output After Training:")
## [1] "Output After Training:"
round(l1,3)
##       [,1]
## [1,] 0.488
## [2,] 0.468
## [3,] 0.449
## [4,] 0.429
## [5,] 0.410
## [6,] 0.391
## [7,] 0.373

Now the idea of a kernel and the so-called kernel trick is to project the input space into a higher dimensional space, like so (sources of pics):

My question
How do I make use of the kernel trick (e.g. with a simple quadratic kernel) so that I get a kernel perceptron, which is able to solve the given classification problem? Please note: This is mainly a conceptual question but if you could also give the necessary code modification this would be great

What I tried so far
I tried the following which works alright but I think that this is not the real deal because it becomes computationally too expensive for more complex problems (the "trick" behind the "kernel trick" is not just the idea of a kernel itself but that you don't have to calculate the projection for all instances):

X <- matrix(c(-3,9,1,
              -2,4,1,
              -1,1,1,
               0,0,1,
               1,1,1,
               2,4,1,
               3,9,1), ncol=3, byrow=T)

y <- c(0,0,1,1,1,0,0)

syn0 <- runif(3,-1,1)

Full Disclosure
I posted this question a week ago on SO but it didn't get much attention. I suspect that here is a better place because it is more a conceptual question than a programming question.

Answer 1

We can construct a "kernel perceptron" by taking the standard perceptron and replacing the inner product $X^\intercal X=\left<X,X\right>$ with the equivalent (due to the "kernel-trick") form K(X,X). This works since we have that the inner product is a map $<\cdot,\cdot>:\mathbb{R}^p\times\mathbb{R}^p\to\mathbb{R}$, which has identical properties to the kernel function $k:\mathbb{R}^p\times\mathbb{R}^p\to\mathbb{R}$. As in the case of the common Gaussian radial basis function kernel (RBF):

$$ K(x_i,x_j)=\exp\left(-\frac{{\left|\left|x_i-x_j\right|\right|}^2}{2\sigma^2}\right) $$

As mentioned in the Wikipedia page on the kernel perceptron, we select a subset of size $M$ of the inputs and use a linear combination of them to produce our output,

$$ f(x) = \sum\limits_i^M \alpha_i y_i K(x,x_i) $$

If you've seen the support vector machine (SVM), you'll notice the identical dual. To select the subset of size $M$ to use, we optimize over $\alpha_i$, which represent whether sample $i$ is a support/basis vector of our solution. In the optimization of the $\alpha_i$ we include the weights $\omega_i$ of the original perceptron optimization.

As to your question about not having to compute the projection, you're correct, your input data matrix $X$ is still 2-dimensional. In the computation of the output we replaced a dot product with the kernel function, and this is where the 'implicit' calculation in the feature space occurs.