I want to create a random variable with a given autocorrelation in R.
The target autocorrelation is defined by: $$acf_{target}=(lag+1)^{(-b)}$$ with $b=1.41519$ which I derived from a natural dataset. You can see the function in the next plot generated with this code:
lag <- seq(0,52)
b <- 1.41519
acf.target <- (lag+1)^(-b)
plot(lag, acf.target, col="green", type="l", xaxs="i", yaxs="i", las=1, lwd=2)
Using the R approach shown in the answer to this question I created a random variable and then filtered the variable with my target autocorrelation function:
n <- 100000
var <- rnorm(n)
var_autocor <- filter(var, filter=acf.target, circular = T)
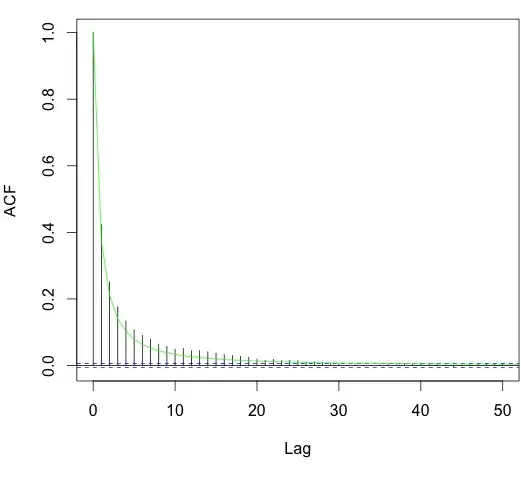
But if I calculate the autocorrelation of var_autocor I get a difference to the target autocorrelation function:
acf(var_autocor)
lines(lag, acf.target, col="green")
I calculate that the acf of the generated variable (var_autocor) has an $b_{result}=1.215306$ which slightly deviates from $b_{target}=1.41519$.
This deviation is more than I want and I don't understand why it appears. Do I use the filter function wrong? Do I have to give additional arguments? Or does someone have a totally different approach to create a random variable with the target autocorrelation?