Would a $(1-\alpha)100\%$ confidence interval for the variance be narrower if we knew the mean a-priori?

Question

Let's say we know the mean of a given distribution. Does this affect the interval estimate of the variance of a random variable (which is otherwise computed using the sample variance)? As in, can we obtain a smaller interval for the same confidence level?

Answer 1

I am not entirely sure my answer is correct, but I would argue there is no general relationship. Here is my point:

Let us study the case where the confidence interval of the variance is well-understood, viz. sampling from a normal distribution (as you indicate in the tag of the question, but not really the question itself). See the discussion here and here.

A confidence interval for $\sigma^2$ follows from the pivot $T=n\hat{\sigma}^2/\sigma^2\sim\chi^2_{n-1}$, where $\hat{\sigma}^2=1/n\sum_i(X_i-\bar{X})^2$. (This is just another way of writing the possibly more familiar expression $T=(n-1)s^2/\sigma^2\sim\chi^2_{n-1}$, where $s^2=1/(n-1)\sum_i(X_i-\bar{X})^2$.)

We thus have \begin{align*} 1-\alpha&=\Pr\{c_l^{n-1}<T<c_u^{n-1}\}\\ &=\Pr\left\{\frac{c_l^{n-1}}{n\hat{\sigma}^2}<\frac{1}{\sigma^2}<\frac{c_u^{n-1}}{n\hat{\sigma}^2}\right\}\\ &=\Pr\left\{\frac{n\hat{\sigma}^2}{c_u^{n-1}}<\sigma^2<\frac{n\hat{\sigma}^2}{c_l^{n-1}}\right\} \end{align*} Hence, a confidence interval is $(n\hat{\sigma}^2/c_u^{n-1},n\hat{\sigma}^2/c_l^{n-1})$. We may choose $c_l^{n-1}$ and $c_u^{n-1}$ as the quantiles $c_u^{n-1}=\chi^2_{n-1,1-\alpha/2}$ and $c_l^{n-1}=\chi^2_{n-1,\alpha/2}$.

(Notice in passing that for whichever variance estimate that, as the $\chi^2$-distribution is skewed, the quantiles will yield a c.i. with the right coverage probability, but not be optimal, i.e. not be the shortest possible ones. For a confidence interval to be as short as possible, we require the density to be identical at the lower and upper end of the c.i., given some additional conditions like unimodality. I do not know if using that optimal c.i. would change things in this answer.)

As explained in the links, $T'=ns_0^2/\sigma^2\sim\chi^2_n$, where $s_0^2=\frac{1}{n}\sum_i(X_i-\mu)^2$ uses the known mean. Hence, we get another valid confidence interval \begin{align*} 1-\alpha&=\Pr\{c_l^{n}<T'<c_u^{n}\}\\ &=\Pr\left\{\frac{ns_0^2}{c_u^{n}}<\sigma^2<\frac{ns_0^2}{c_l^{n}}\right\} \end{align*} Here, $c_l^{n}$ and $c_u^{n}$ will thus be quantiles from the $\chi^2_n$-distribution.

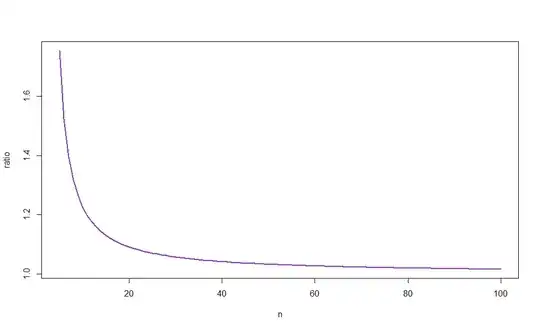
The widths of the confidence intervals are $$ w_T=\frac{n\hat{\sigma}^2(c_u^{n-1}-c_l^{n-1})}{c_l^{n-1}c_u^{n-1}} $$ and $$ w_{T'}=\frac{ns_0^2(c_u^{n}-c_l^{n})}{c_l^{n}c_u^{n}} $$ The relative width is $$ \frac{w_T}{w_{T'}}=\frac{\hat{\sigma}^2}{s_0^2}\frac{c_u^{n-1}-c_l^{n-1}}{c_u^{n}-c_l^{n}}\frac{c_l^{n}c_u^{n}}{c_l^{n-1}c_u^{n-1}} $$ We know that $\hat{\sigma}^2/s_0^2\leq1$ as the sample mean minimizes the sum of squared deviations. Beyond that, I see few general results regarding the width of the interval, as I am not aware of clear-cut results how differences and products of upper and lower $\chi^2$ quantiles behave as we increase degrees of freedom by one (but see the figure below).

For example, letting

$$ r_n:=\frac{c_u^{n-1}-c_l^{n-1}}{c_u^{n}-c_l^{n}}\frac{c_l^{n}c_u^{n}}{c_l^{n-1}c_u^{n-1}},$$ we have

$$r_{10}\approx1.226$$ for $\alpha=0.05$ and $n=10$, meaning that the c.i. based on $\hat{\sigma}^2$ will be shorter if $$ \hat{\sigma}^2\leq\frac{s_0^2}{1.226} $$

Using the code below, I ran a little simulation study suggesting that the interval based on $s_0^2$ will win most of the time. (See the link posted in Aksakal's answer for a large-sample rationalization of this result.)

The probability seems to stabilize in $n$, but I am not aware of an analytical finite-sample explanation:

    rm(list=ls())

IntervalLengthsSigma2 <- function(n,alpha=0.05,reps=100000,mu=1) {
  cl_a <- qchisq(alpha/2,df = n-1)
  cu_a <- qchisq(1-alpha/2,df = n-1)
  cl_b <- qchisq(alpha/2,df = n)
  cu_b <- qchisq(1-alpha/2,df = n)

  winners02 <- rep(NA,reps)

  for (i in 1:reps) {
    x <- rnorm(n,mean=mu)
    xbar <- mean(x)
    s2 <- 1/n*sum((x-xbar)^2)
    s02 <- 1/n*sum((x-mu)^2)

    ci_a <- c(n*s2/cu_a,n*s2/cl_a)
    ci_b <- c(n*s02/cu_b,n*s02/cl_b)

    winners02[i] <- ifelse(ci_a[2]-ci_a[1]>ci_b[2]-ci_b[1],1,0)  
  }
  mean(winners02)
}

nvalues <- matrix(seq(5,200,by=10)) 
plot(nvalues,apply(nvalues,1,IntervalLengthsSigma2),pch=19,col="lightblue",type="b")

The next figure plots $r_n$ against $n$, revealing (as intuition would suggest) that the ratio tends to 1. As, moreover, $\bar{X}\to_p\mu$ for $n$ large, the difference between the widths of the two c.i.s will therefore vanish as $n\to\infty$. (See again the link posted in Aksakal's answer for a large-sample rationalization of this result.)

Answer 2

Let me first set up the problem. We know the population mean. This is a very important point to make in the very beginning, because without it, we'll not have a meaningful answer.

I'll explain why. Let's say we have a sample and don't know the population mean. We have a usual estimator of the variance: $$\sigma=\frac{1}{n-1}sum_i(x_i-\bar x)^2$$

Now, we're told that the population mean is $\mu$. Our first instinct is to plug it into the variance estimator: $$\sigma'=\frac{1}{n}sum_i(x_i-\mu)^2$$

Notice, that it's a different estimator now! It has different denominator etc. It has a different variance itself.

However, is it right to compare $Var[\sigma]$ and $Var[\sigma']$? No, it's NOT.

We have to compare $Var[\sigma|E[x_i]=\mu]$ and $Var[\sigma'|E[x_i]=\mu]$. In other words we have to compare the variance of these two estimators conditional on the knowledge of the population mean! Otherwise, we'll fall into @Scortchi's paradox.

When you got new information, i.e. $E[x_i]=\mu$, you have to include it in the estimate of $Var[\sigma]$! This solves @Scortchi's paradox in his comment directly. The equations that I saw so far in answers do not include the knowledge of $\mu$ into the C.I. or variance of the variance estimator $\sigma$. In @Scortchi's example knowing that $\bar x>>\mu$ would lead to a revision of C.I. of $\sigma$.

Hence, my answer here follows the set up I jest described.

Yes, the confidence interval would have been narrower.

Philosophically, knowing mean of the population is an additional information, so the uncertainty must be smaller in this case.

Example: if your distribution is Poisson, then variance is equal mean. Hence, knowing mean you know the variance too, and the confidence interval shrinks to a point. There's no interval.

UPDATE: Look at this paper: "Estimating a Population Variance with Known Mean" by Zhang, 1996. He compares the standard estimate of variance $\frac{1}{n-1}\sum_i(x_i-\bar x)^2$ vs. the one using the knowledge of the population mean $\frac{1}{n}\sum_i(x_i-\mu)^2$. He comes to the same conclusion: the variance of the latter estimate is smaller than that of the former, i.e. the confidence interval of variance estimate would be narrower. He also shows that the advantage disappears when the sample size tends to infinity.

I think this paper is the definitive answer to your question.

Answer 3

Extending @Cristoph Hanck's answer a little, & adapting his code …

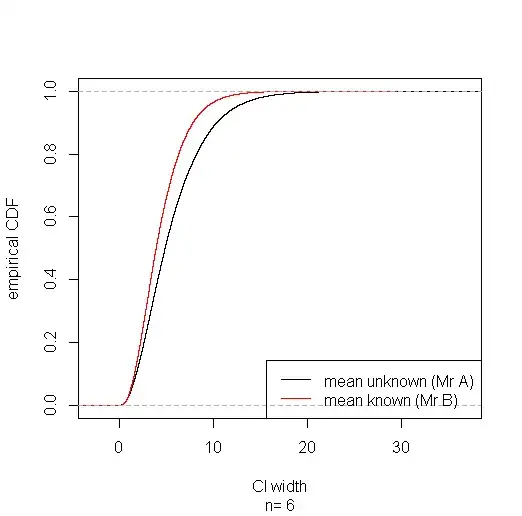
Suppose Mr A is ignorant of the true mean, or of statistics, & Mr B is ignorant of neither. It might seem odd, unfair even, that Mr A can obtain a shorter confidence interval for the variance using the pivot $T$ than Mr B using the pivot $T'$. But in the long run Mr B wins in rather a strong sense: his confidence intervals are stochastically narrower—for any width $w$ you care to specify, the proportion of Mr B's CIs narrower than $w$ is greater than the proportion of Mr A's.

Collecting together the subset of cases where Mr A's CI comes out narrower shows that in these he's got lower coverage (about 91%); but he pays for it with higher coverage (about 96%) in the subset of cases where his interval comes out wider, getting the correct (95%) coverage overall. Of course Mr A doesn't know when his CI's in which subset. And a sly Mr C who knows the true mean & picks $T$ or $T'$ according to which results in the narrowest CI will eventually be exposed when his intervals fail to maintain their supposed 95% coverage.

IntervalLengthsSigma2 <- function(n,alpha=0.05,reps=100000,mu=1) {
  cl_a <- qchisq(alpha/2,df = n-1)
  cu_a <- qchisq(1-alpha/2,df = n-1)
  cl_b <- qchisq(alpha/2,df = n)
  cu_b <- qchisq(1-alpha/2,df = n)

  winners02 <- rep(NA,reps)
  width.a <- rep(NA,reps)
  width.b <- rep(NA,reps)
  sigma2.in.a <- rep(NA,reps)
  sigma2.in.b <- rep(NA,reps)

  for (i in 1:reps) {
    x <- rnorm(n,mean=mu)
    xbar <- mean(x)
    s2 <- 1/n*sum((x-xbar)^2)
    s02 <- 1/n*sum((x-mu)^2)

    ci_a <- c(n*s2/cu_a,n*s2/cl_a)
    ci_b <- c(n*s02/cu_b,n*s02/cl_b)

    winners02[i] <- ifelse(ci_a[2]-ci_a[1]>ci_b[2]-ci_b[1],1,0) 
    ci_a[2]-ci_a[1] -> width.a[i]
    ci_b[2]-ci_b[1] -> width.b[i]
    ifelse(ci_a[1]< 1 & ci_a[2] > 1, 1, 0) -> sigma2.in.a[i]
    ifelse(ci_b[1]< 1 & ci_b[2] > 1, 1, 0) -> sigma2.in.b[i]
  }

 list(n=n, width.a=width.a,width.b=width.b, sigma2.in.a=sigma2.in.a, sigma2.in.b=sigma2.in.b, winner=winners02)
}

# simulate for sample size of 6
IntervalLengthsSigma2(n=6) -> sim

# plot empirical CDFs of CI widths for mean known & mean unknown
plot(ecdf(sim$width.a), xlab="CI width", ylab="empirical CDF", sub=paste("n=",sim$n), main="")
lines(ecdf(sim$width.b), col="red")
legend("bottomright", lty=1, col=c("black", "red"), legend=c("mean unknown (Mr A)", "mean known (Mr B)"))

# coverage with mean unknown:
mean(sim$sigma2.in.a)
# coverage with mean unknown when CI is narrower than with mean known:
mean(sim$sigma2.in.a[sim$winner==0])
# coverage with mean unknown when CI is wider than with mean known:
mean(sim$sigma2.in.a[sim$winner==1])

# coverage with mean known:
mean(sim$sigma2.in.b)
# coverage with mean known when CI is wider than with mean unknown:
mean(sim$sigma2.in.b[sim$winner==0])
# coverage with mean known when CI is narrower than with mean unknown;
mean(sim$sigma2.in.b[sim$winner==1])

Answer 4

I can't comment but Aksakal's sweeping statement "knowing mean of the population is an additional information, so the uncertainty must be smaller in this case" is not self evident.

In the normally distributed case, the maximum likelihood estimator of the variance when $\mu$ is unknown:

$$ \frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})^2 $$

has uniformly lower variance than

$$ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2 $$

for any values of $\mu, \sigma$