45

I was reading the paper ImageNet Classification with Deep Convolutional Neural Networks and in section 3 were they explain the architecture of their Convolutional Neural Network they explain how they preferred using:

non-saturating nonlinearity $f(x) = max(0, x). $

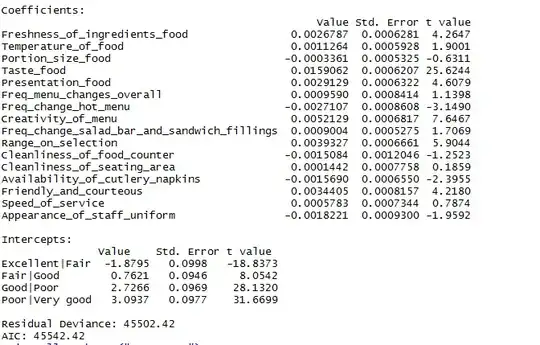
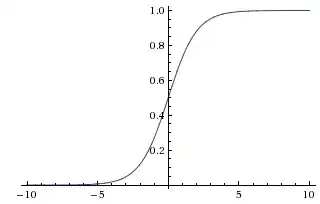
because it was faster to train. In that paper they seem to refer to saturating nonlinearities as the more traditional functions used in CNNs, the sigmoid and the hyperbolic tangent functions (i.e. $f(x) = tanh(x)$ and $f(x) = \frac{1}{1 + e^{-x}} = (1 + e^{-x})^{-1}$ as saturating).

Why do they refer to these functions as "saturating" or "non-saturating"? In what sense are these function "saturating" or "non-saturating"? What do those terms mean in the context of convolutional neural networks? Are they used in other areas of machine learning (and statistics)?

Charlie Parker
  • 5,836
  • 11
  • 57
  • 113
  • I also found [this quora answer](https://www.quora.com/Why-would-a-saturated-neuron-be-a-problem) very helpful. – Nathan Jul 04 '19 at 21:18
  • 1
    It should be noted that the main important difference is not the form of the function and neither really its squashing behaviour but that the non-saturating ones don't have vanishing gradients if the activations for some reason get out of control. And you need gradients to do gradient descent. The Rectified Linear unit (ReLU), what you refer to by the max() formula, has a decent gradient at all values (pun intended ;). – BjornW Jan 24 '21 at 14:03

3 Answers3

43

Intuition

A saturating activation function squeezes the input.

Definitions

  • $f$ is non-saturating iff $ (|\lim_{z\to-\infty} f(z)| = +\infty) \vee (|\lim_{z\to+\infty} f(z)| = +\infty) $
  • $f$ is saturating iff $f$ is not non-saturating.

These definitions are not specific to convolutional neural networks.

Examples

The Rectified Linear Unit (ReLU) activation function, which is defined as $f(x)=max(0,x)$ is non-saturating because $\lim_{z\to+\infty} f(z) = +\infty$:

enter image description here

The sigmoid activation function, which is defined as $f(x) = \frac{1}{1 + e^{-x}}$ is saturating, because it squashes real numbers to range between $[0,1]$:

enter image description here

The tanh (hyperbolic tangent) activation function is saturating as it squashes real numbers to range between $[-1,1]$:

enter image description here

(figures are from CS231n, MIT License)

Stoner
  • 183
  • 1
  • 2
  • 14
Franck Dernoncourt
  • 42,093
  • 30
  • 155
  • 271
  • 1
    ah, nice makes sense! I know this wasn't my original question, but what is that property important in the context of ML and CNNs? – Charlie Parker Sep 28 '15 at 15:43
  • For ANNs, to avoid having one unit with a large output that impacts too much the ANN's output layer. – Franck Dernoncourt Sep 28 '15 at 18:03
  • whats the difference between tan and sigmoid? both of them squash the numbers in a closed range! I dont get it, Can you elaborate this abit more? I'm kind of bad in mathematics . (by the way I'm coming from a CNN perspective ) – Hossein Feb 17 '16 at 11:09
  • @FranckDernoncourt Did you mean saturating for tanh activation function? I guess there is a typo? :) – CoderSpinoza Mar 24 '16 at 04:44
  • Can someone tell me why they chose this word? Is there an intuition behind that? Is it an import from a foreign language or another field? – crackpotHouseplant Apr 08 '17 at 05:06
  • 3
    @tenCupMaximum: To *saturate* means to fill up to a point where no more can be added. In the context of a saturating function, it means that after a certain point, any further increase in the function's input will no longer cause a (meaningful) increase in its output, which has (very nearly) reached its maximum value. The function at that point is "all filled up", so to speak (or *saturated*). – Ruben van Bergen Oct 10 '17 at 11:16
1

The most common activation functions are LOG and TanH. These functions have a compact range, meaning that they compress the neural response into a bounded subset of the real numbers. The LOG compresses inputs to outputs between 0 and 1, the TAN H between -1 and 1. These functions display limiting behavior at the boundaries.

At the border the gradient of the output with respect to the input ∂yj/∂xj is very small. So Gradient is small hence small steps to convergence hence longer time to converge.

Pradi KL
  • 119
  • 3
1

In the neural network context, the phenomenon of saturation refers to the state in which a neuron predominantly outputs values close to the asymptotic ends of the bounded activation function.

So, saturation refers to behaviour of a neuron in a neural network after a given period of training/for a given range of input, and only neurons with bounded limits are susceptible to saturation (and by extension, such functions are sometimes referred to as 'saturating' even if in a particular instance they have not 'saturated').

Saturating functions include:

Type Examples
Limited as x approaches infinity and minus infinity Sigmoid, tanh
Limited only in one direction $\max(x,c)$

Non saturating functions include:

Type Examples
Unbounded functions identity, $\sinh$, $abs$
Periodic functions sin, cos

So in your example, a "non-saturating nonlinearity" means a "non-linear function with no limit as x approaches infinity".

brazofuerte
  • 737
  • 4
  • 19