I have come across the term "saturation" in the context of neural networks and I can't find a straightforward definition for it. for instance:
Because linear units do not saturate, they pose little difficulty for gradient- based optimization algorithms
Does someone have a good definition for "saturation"?
An activation function $h(x)$ with derivative $h_0 (x)$ is said to right (resp. left) saturate if its limit as $x → ∞$ (resp. $x → −∞$) is zero. An activation function is said to saturate (without qualification) if it both left and right saturates. Most common activation functions used in recurrent networks (for example, tanh and sigmoid) are saturating. In particular they are soft saturating, meaning that they achieve saturation only in the limit.
Let $c$ be a constant such that $x > c$ implies $h_0(x) = 0$ and left hard saturates when $x < c$ implies $h_0(x) = 0, ∀x.$ We say that h(·) hard saturates (without qualification) if it both left and right hard saturates. An activation function that saturates but achieves zero gradient only in the limit is said to soft saturate.
We can construct hard saturating versions of soft saturating activation functions by taking a first-order Taylor expansion about zero and clipping the results to an appropriate range.
For example, expanding tanh and sigmoid around 0, with $x ≈ 0$, we obtain linearized functions $u_t$ and $u_s$ of tanh and sigmoid respectively:
$sigmoid(x) ≈ u_s(x) = 0.25x + 0.5$
$tanh(x) ≈ u_t(x) = x$
Clipping the linear approximations result to,
$hard-sigmoid(x) = max(min(u_s(x), 1), 0)$
$hard-tanh(x) = max(min(u_t(x), 1), − 1)$
The motivation behind this construction is to introduce linear behavior around zero to allow gradients to flow easily when the unit is not saturated, while providing a crisp decision in the saturated regime.
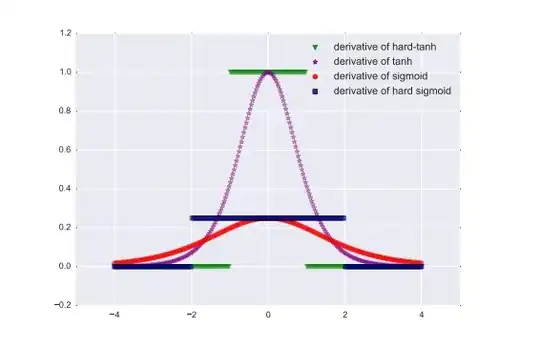
The ability of the hard-sigmoid and hard-tanh to make crisp decisions comes at the cost of exactly 0 gradients in the saturated regime. This can cause difficulties during training: a small but not infinitesimal change of the pre-activation (before the nonlinearity) may help to reduce the objective function, but this will not be reflected in the gradient.
