Can I calculate this Bayesian line without needing to simulate every point?

Question

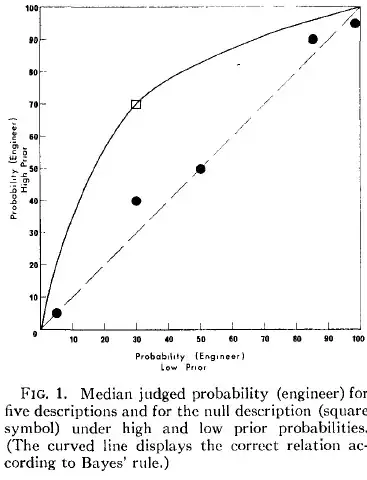
Kahneman and Tversky mention that in this graph the value of (high prior group)/(low prior group) should be 5.44.

Kahneman and Tversky call the curved line a "Bayesian line" and I believe I understand how it works. For instance, if the probability at the low prior is 0.5, then the odds are 1. I then take 1 * 5.44 = 5.44, and from there convert back to probabilities 5.44/(5.44+1) = 0.85. Indeed, the y-value of the curved line is approximately 0.85 at the point where the low prior is 0.5.

However, let's say I have another situation and I know that the (high prior group)/(low prior group) should be something else, e.g. 2. I could easily write a program to calculate the correct value for the curved line for low prior group = 0.01, 0.02, 0.03, and so on up to 1. However, I wonder if there is perhaps a more elegant solution.

Kahneman, D., & Tversky, A. (1973). On the psychology of prediction. Psychological review, 80(4), 237.

Answer 1

As Kahneman & Tversky explain, and as you have accurately stated, the plot converts a probability $p$ (on the horizontal axis) to odds, multiplies that by an odds ratio $\alpha = 5.44$, then converts it back to a probability $q$ plotted on the vertical axis. It shows how Bayes' Rule works for a fixed odds ratio applied to a full range of prior probabilities $p$ to produce the posterior probability $q$.

Because the odds of a probability $p$ in the range $(0,1)$ is

$$y = \frac{p}{1-p},$$

simple algebra finds the probability in terms of odds,

$$p = \frac{y}{1+y}.\tag{1}$$

Applying $(1)$ to an odds of $\alpha y$ instead of $y$ gives

$$q = \frac{\alpha y}{1 + \alpha y} = \frac{\alpha p}{1-p + \alpha p}.$$

That is the equation of the graph. It is what your program should calculate for any $p$ between $0$ and $1$. (Evidently, $p=0$ should correspond to $q=0$ and $p=1$ to $q=1$ to make the plots continuous at their endpoints.)

To illustrate, here are plots for various odds ratios greater than $1$: