1

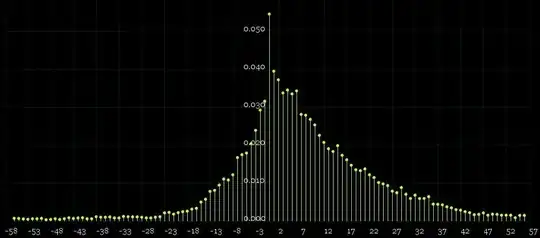
If a probability distribution has, say, 112 bins with around 29000 samples, with the maximum probability of a bin being less than 0.05, is the Jarque-Bera test an effective measure of conformance to a Normal distribution?

I'm working with univariate data, whose probability distribution 'looks' normal, with some deviation. However, the Jarque-Bera test for normality indicates that it is not normal.

Also, since n ~ 29000, the JB statistic is inflated to a ridiculous value like 1474523. Am I doing something wrong? Any help would be most welcome.

The Jarque Bera statistics and a histogram for these data are:

n = 28535.0
Skewness = -4.24685767755943
Kurtosis = 37.1765663807246
JB statistic = 1474523.40413686

Histogram

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
ipadawan
  • 31
  • 1
  • You can look at the probability distribution here: http://d2o7bfz2il9cb7.cloudfront.net/main-qimg-1e9b09e9dddbf6650ff1937f46ba9f57 – ipadawan Oct 17 '11 at 15:43
  • 1
    That's not even remotely normal! The enormous JB statistic is merely telling you what is plainly obvious in the histogram. – whuber Oct 17 '11 at 15:57

2 Answers2

1

I'm working with univariate data, whose probability distribution 'looks' normal, with some deviation. However, the Jarque-Bera test for normality indicates that it is not normal.

You have relied on a visual 'measure' for inferring normality. I think you should be equipped with other visualization tools that must be used when looking for normality.

a) Q-Q plot- have a look at this answer on this site.

A quantile means the fraction of points below that value. Ex- 0.25 quantile means the value below which 25% of the data is present.

b) Normal probability plot

The data are plotted against a theoretical normal distribution in such a way that the points should form an approximate straight line. Departures from this straight line indicates departure from normality.

c) Histogram

The histogram graphically shows many things about a distribution that includes the center (i.e., the location) of the data, spread (i.e., the scale) of the data, skewness of the data, presence of outliers. But one needs to be careful with this!

naive
  • 899
  • 1
  • 9
  • 14
0

Partially answered in comments:

That's not even remotely normal! The enormous JB statistic is merely telling you what is plainly obvious in the histogram. – whuber

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467