Variance-covariance matrix of logit with matrix computation

Question

I'm trying to obtain the variance-covariance matrix of a logistic regression:

mydata <- read.csv("https://stats.idre.ucla.edu/stat/data/binary.csv")
mylogit <- glm(admit ~ gre + gpa, data = mydata, family = "binomial")

through matrix computation. I have been following the example published here for the basic linear regression

X <- as.matrix(cbind(1, mydata[,c('gre','gpa')]))
beta.hat <- as.matrix(coef(mylogit))
Y <- as.matrix(mydata$admit)
y.hat <- X %*% beta.hat

n <- nrow(X)
p <- ncol(X)

sigma2 <- sum((Y - y.hat)^2)/(n - p)        
v <- solve(t(X) %*% X) * sigma2

But then my var/cov matrix doesn't not equals the matrix computed with vcov()

v == vcov(mylogit)

1   gre   gpa
1   FALSE FALSE FALSE
gre FALSE FALSE FALSE
gpa FALSE FALSE FALSE

Did I miss some log transformation?

Answer 1

@Deep North: You are right, there should not be a 'n'

The covariance matrix of a logistic regression is different from the covariance matrix of a linear regression.

1. Linear Regression:
2. Logistic Regression:

Where W is diagonal matrix with

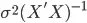
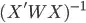
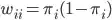
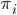is the probability of event=1 at the observation level

Answer 2

The covariance for logistic regression from subra is correct. But $w_{ii}=\hat{\pi_i}(1-\hat{\pi_i})$. There should not have a $n_i$. ref. David W. Hosmer Applied Logistic Regression (2nd Editiion) p35 and p41 formular(2.8)

I revised your program and compare with variance estimation, they are close but not the same.

 library(Matrix)
 library(sandwich)
 mydata <- read.csv("http://www.ats.ucla.edu/stat/data/binary.csv")
 mylogit <- glm(admit ~ gre + gpa, data = mydata, family = "binomial")
 X <- as.matrix(cbind(1, mydata[,c('gre','gpa')]))
 n <- nrow(X)

 pi<-mylogit$fit

 w<-pi*(1-pi)

 v<-Diagonal(n, x = w)
 var_b<-solve(t(X)%*%v%*%X)
 var_b

         x 3 Matrix of class "dgeMatrix"
          [,1]          [,2]          [,3]
[1,]  1.1558251135 -2.818944e-04 -0.2825632388
[2,] -0.0002818944  1.118288e-06 -0.0001144821
[3,] -0.2825632388 -1.144821e-04  0.1021349767


vcov(mylogit)

         (Intercept)           gre           gpa
(Intercept)  1.1558247051 -2.818942e-04 -0.2825631552
gre         -0.0002818942  1.118287e-06 -0.0001144821
gpa         -0.2825631552 -1.144821e-04  0.1021349526

They are the same at the first five digits

Answer 3

mydata <- read.csv("http://www.ats.ucla.edu/stat/data/binary.csv")
mylogit <- glm(admit ~ gre + gpa, data = mydata, family = "binomial")

X <- as.matrix(cbind(1, mydata[,c('gre','gpa')]))
beta.hat <- as.matrix(coef(mylogit))

require(slam)
p <- 1/(1+exp(-X %*% beta.hat))
V <- simple_triplet_zero_matrix(dim(X)[1])
diag(V) <- p*(1-p)
IB <- matprod_simple_triplet_matrix(t(X), V) %*% X
varcov_mat <- solve(IB)

round(solve(IB),4) == round(vcov(mylogit),4)

# 1  gre  gpa
# 1   TRUE TRUE TRUE
# gre TRUE TRUE TRUE
# gpa TRUE TRUE TRUE