CART: Selection of best predictor for splitting when gains in impurity decrease are equal?

Question

My question deals with Classification trees. Consider the following example from the Iris data set:

I want to manually select the best predictor for the first split. According to the CART algorithm, the best feature to make a split is the one that maximizes the decrease in partition impurity, also called Gini gain:

$GiniGain(N,X)=Gini(N)-\frac{\lvert N_{1} \rvert }{\lvert N \rvert }Gini(N_{1})-\frac{\lvert N_{2} \rvert }{\lvert N \rvert }Gini(N_{1})$

Where $X$ is a given feature, $N$ is the node on which the split is to be made, and $N_{1}$ and $N_{2}$ are the two child nodes created by splitting $N$. $\lvert . \rvert $ is the number of elements in a node.

And $Gini(N)=1-\sum_{k=1}^{K}p_{k}^2$, where $K$ is the number of categories in the node

Now, since making a split based on petal width (axis #1) and petal length (axis #2) yields the same partition (all Setosa flowers are separated from the non-Setosa), the GinGain scores will be exactly the same for each predictor. So how does the CART algorithm decide which one is best?

Intuitively, one can see that splitting on petal length (2) is associated with the greatest "margin", hence petal length should be chosen (it is actually what happens when implementing rpart in R), but nothing in $GiniGain$ measures margin, so the decision must be based on something else.

Related thread but without the answer to my question.

Related thread without any answer.

Answer 1

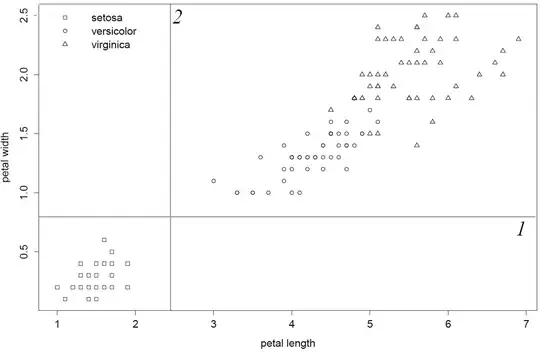
I confess to be a mediocre c-code interpreter and this old code is not not user-friendly. That said I went through the source code and made these observations which makes me quite sure to say: "rpart literally picks the first and best variable column". As column 1 and 2 produce inferior splits, petal.length will be first split-variable because this column is before petal.width in data.frame/matrix. Lastly, I show this by inverting column order such that petal.with will be first split-variable.

In in the c source file "bsplit.c" in source code for rpart I quote from line 38:

 * test out the variables 1 at at time
me->primary = (pSplit) NULL;
for (i = 0; i < rp.nvar; i++) {

... thus iterating in a for loop starting from i=1 to rp.nvar a loss function will be called to scan all split by one variable, inside gini.c for "non-categorical split" line 230 the best found split is updated if a new split is better. (This could also be a user defined loss-function)

if (temp < best) {
        best = temp;
        where = i;
        direction = lmean < rmean ? LEFT : RIGHT;
}

and last line 323, the improvement for best split by a variable is calculated...

*improve = total_ss - best

...back in bsplit.c the improvement is checked if larger than what previously seen, and only updated if larger.

if (improve > rp.iscale)
rp.iscale = improve;        /* largest seen so far */

My impression on this is that the first and best (of possible ties will be chosen), because only if new break point have a better score it will be saved. This concerns both the first best break point found and the first best variable found. Break points seems not to be scanned simply left to right in gini.c so the first found tying break point may be tricky to predict. But variables are very predictable scanned from first column to last column.

This behavior is different from the randomForest implementation where in classTree.c the following solution is used:

/* Break ties at random: */
if (crit == critmax) {
    if (unif_rand() < 1.0 / ntie) {
        *bestSplit = j;
        critmax = crit;
        *splitVar = mvar;
    }
    ntie++;
}

very lastly I confirm this behaviour by flipping the columns of iris, such that petal.width is chosen first

library(rpart)
data(iris)
iris = iris[,5:1]  #flip/flop", invert order of columns columns
obj = rpart(Species~.,data=iris)
print(obj) #now petal width is first split 


1) root 150 100 setosa (0.33333333 0.33333333 0.33333333)  
  2) Petal.Width< 0.8 50   0 setosa (1.00000000 0.00000000 0.00000000) *
  3) Petal.Width>=0.8 100  50 versicolor (0.00000000 0.50000000 0.50000000)  
    6) Petal.Width< 1.75 54   5 versicolor (0.00000000 0.90740741 0.09259259) *
    7) Petal.Width>=1.75 46   1 virginica (0.00000000 0.02173913 0.97826087) *

...and flip back again

iris = iris[,5:1]  #flop/flip", revert order of columns columns
obj = rpart(Species~.,data=iris)
print(obj) #now petal length is first split 
1) root 150 100 setosa (0.33333333 0.33333333 0.33333333)  
  2) Petal.Length< 2.45 50   0 setosa (1.00000000 0.00000000 0.00000000) *
  3) Petal.Length>=2.45 100  50 versicolor (0.00000000 0.50000000 0.50000000)  
    6) Petal.Width< 1.75 54   5 versicolor (0.00000000 0.90740741 0.09259259) *
    7) Petal.Width>=1.75 46   1 virginica (0.00000000 0.02173913 0.97826087) *