If $X$ and $Y$ are random variables whose joint density function
$f_{X,Y}(x,y)$ has circular symmetry about the origin, that is,
the value of $f_{X,Y}$ at any point $(x,y)$ in the plane depends
not on the individual values of $x$ and $y$ but only on
$r = \sqrt{x^2+y^2}$, the (Euclidean) distance of the point $(x,y)$
from the origin, then we can write
$f_{X,Y}(x,y)$ as a function $g(r)$ of $r$ alone. Note that
$g(r) = f_{X,Y}(r,0)=f_{X,Y}(0,r)$. Then, with
$R = \sqrt{X^2+Y^2}$ denoting the distance of the random point $(X,Y)$
from the origin, we have that the density of $R$ is given by
$$f_R(r) = 2\pi r g(r), \quad 0 \leq r < \infty.\tag{1}$$
In the special case when $X$ and $Y$ are independent $N(0,\sigma^2)$
random variables, we have that
$$f_{X,Y} (x,y)
= \frac{1}{2\pi\sigma^2}\exp\left(-\frac{1}{2\sigma^2}
\left(x^2+y^2\right)\right)
= \frac{1}{2\pi\sigma^2}\exp\left(-\frac{r^2}{2\sigma^2}\right)\tag{2}$$
giving the Rayleigh density
$$f_R(r) = \frac{r}{\sigma^2}\exp\left(-\frac{r^2}{2\sigma^2}\right),
\quad 0 \leq r < \infty\tag{3}$$
that you mentioned. But you should understand clearly that this is a
special case. Indeed, if $X$ and $Y$ have a circularly symmetric
density, then they are independent if and only if they are
zero-mean normal random variables with the same variance. So, $(3)$
holds only in this special case.
A proof of $(1)$ in the general case is straightforward. We have that for
$a \geq 0$,
\begin{align}F_R(a) &= P\{R \leq a\}\\
&= P\{\sqrt{X^2+Y^2} \leq a\}\\
&= \iint_{\sqrt{x^2+y^2} \leq a}f_{X,Y}(x,y)\,\mathrm dx\,\mathrm dy
& \scriptstyle{\text{integral over circle of radius }a}\\
&= \int_{r=0}^a \int_{\theta=0}^{2\pi} g(r)\cdot r\,\mathrm d\theta
\cdot \mathrm dr & \scriptstyle{\text{change to polar coordinates}}\\
&= \int_{r=0}^a 2\pi r g(r)\, \mathrm dr
& \scriptstyle{\text{inner integral has value }2\pi}
\end{align}
which upon comparison to
$\displaystyle F_R(a) = \int_{-\infty}^a f_R(r)\,\mathrm dr
= \int_0^a f_R(r)\,\mathrm dr$ leads us to $(1)$.
For more details on this calculation, as well as what happens
when $X$ and $Y$ do not enjoy circular symmetry, see Examples 4.6.2
(p. 185) and 4.7.6 (p. 192) in the
Course Notes for ECE 313. I will also recommend these Notes for
gaining a solid understanding of probability theory at the undergraduate
level. (end of commercial).
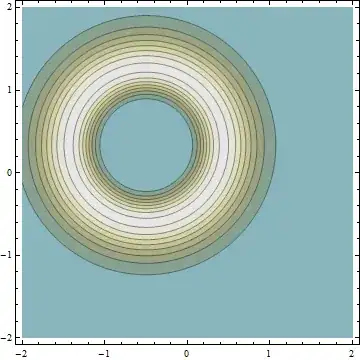
Finally, in response to your question about the "hole in the middle",
the function $g(r)$ would have value $0$ for small values of $r$
(corresponding to the hole). Since $(1)$ gives the density function
of the magnitude $R$ of the distance from the origin, you should
be able to compute the variance of $R$ by yourself.
 ]
]