Fourier data with non-integer periods, correcting for phase bias

Question

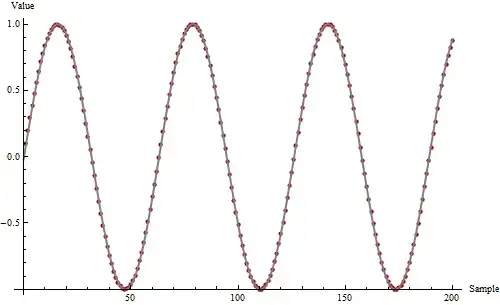
I have data that I believe is sinusoidal, but I don't have an integral number of periods. How do I find the "best fit" Sin/Cos function, compensating for this and for the ugly constant that appears? EXAMPLE:

• Here is some data that follows a sinusoidal pattern (Mathematica format)

  t4 = N[Table[Sin[3.17*2*Pi*x/200], {x,1,200}]];

• Now, using just t4, I want to get back Sin[3.17*2*Pi*x/200] or the equivalent.

• Note that Mean[t4] is non-zero (it's about 0.0281886). The analyses I've tried so far "pull out" this mean (like "0.0281886 + ..."). This is bad because it's unlikely I'll get back to my original form with that constant pulled out.

• Using j0ker5's excellent technique from https://stackoverflow.com/questions/4463481/continuous-fourier-transform-on-discrete-data-using-mathematica I can compensate for the non-integral period and get:

  0.0281886 + 0.983639 Cos[1.49867 - 0.0992743 x]

Note that the x term is 3.16*2*Pi*x/200, very close to my original.

• I modified j0ker5's technique slightly. The actual function I used to get the above:

superfourier2[data_] :=Module[ 
 {pdata, n, f, pos, fr, frpos, freq, phase, coeff}, 
 pdata = data; 
 n = Length[data]; 
 f = Abs[Fourier[pdata]]; 
 pos = Ordering[-f, 1][[1]] - 1; 
 fr = Abs[Fourier[pdata*Exp[2*PiIposRange[0,n-1]/n], 
      FourierParameters -> {0, 2/n}]]; 
 frpos = Ordering[-fr, 1][[1]]; 
 freq = (pos + 2(frpos - 1)/n); 
 phase = Sum[Exp[freq*2*PiIx/n]*pdata[[x]], {x,1,n}]; 
 coeff =  N[{Mean[data], 2*Abs[phase]/n, freq*2*Pi/n, Arg[phase]}]; 
 Function[x, Evaluate[coeff[[1]] + coeff[[2]]*Cos[coeff[[3]]*x - coeff[[4]]]]] 
] 

• In addition to the bad constant term, note that adding "0.983639*Cos[1.49867 - 0.0992743 x]" for x=1..200 yields 0.0279175*200, which I'm convinced makes things worse, not better.

• I believe the 0.0279175*200 sum from the cosine and the 200*0.0281886 from the mean can somehow "cancel" to yield back my pure Sin[] function.

Thoughts?

Answer 1

The periodogram will estimate the periods. It will also handle noisy data and pick out multiple sinusoidal components of different period.

A quick and dirty Mathematica calculation is

data = N[Table[Sin[3.17*2*Pi*x/200], {x, 1, n}]];
welch = 1 - (2 (Range[n] - (n - 1)/2)/(n + 1))^2;
fData = Append[Abs[Fourier[welch data]]^2 / (Plus @@ (welch^2)), 0];
fData = (fData + Reverse[fData])/2;
fData = fData / (Plus @@ fData);

(You don't really need the last two steps, but I kept them in because they produced the illustrations below.)

Here's a plot of the important part of the periodogram in this example:

The points are the periodogram values while the line is a quick smooth (I used a polynomial interpolator of order 5, but with more time would apply a Gaussian kernel smooth):

f = Interpolation[Log[fData], InterpolationOrder -> 5];
period = x /. (NMaximize[f[x + 1], x] // Last)

The maximum of the smoothed value occurs at $3.17661$, whose closeness to $3.17$ is evidence of the promise of this technique.

Once you have an estimate of the period, it's straightforward to find the phase and amplitude (use nonlinear least squares, or run a tight bandpass filter over the Fourier transform and invert it).

NonlinearModelFit[data, a Sin[\[Phi] + period*2*Pi*x/200], {a, \[Phi]}, x]

The estimated amplitude ($a$) is $1.00011$ and phase ($\phi$) is $0.0212758$, both close to the actual values of $1$ and $0$, respectively. (The phase estimate is less than one sampling interval ($2\pi/200 = 0.0314$) from the correct phase, which is about as good as one can expect.) Compare the data to this fit:

The residuals exhibit some quasi-periodicity (attributable to cutting off the data at a non-integral period) and range from $-0.018$ to $0.021$.