I have a question about analyzing the data from a coupled pendulum.
I have measured the amplitude $\psi(t)$ which is expected to be a beat and I want to measure the period. The ideal plot would be something like this.
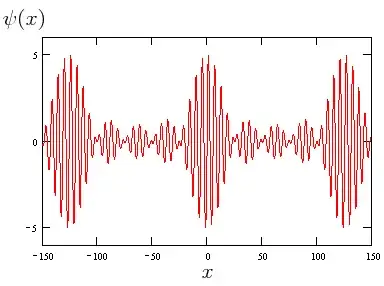
I have to measure the period of the envelope and the individual components.
The image is ideal, because the amplitude will be decreasing slowly with time.
So I would like to know the best method to calculate the period and its error. I have considered these options:
Fast Fourier Transform (FFT): The problem I see is that it's not a totally periodic function, so it might introduce more error. And I've read that the error is related to the covariance matrix, but I don't understand it.
Measuring the distance between maxima/minimum: This would not be affected by the damping, but you would waste many points.