How to interpret this QQ plot?

Question

I have ran a QQ plot on R on my data using

par(mfrow=c(1,2))
par(pty="s")
qqnorm(TEDS$LST1); qqline(TEDS$LST1)

which gave me this:

The histogram of the data showed a positive skew to left, but I do not know how to interpret the QQ plot. Why are the data points clustering along the line? and does the straight tail at the bottom signify the left skew that I see in the histogram?

Answer 1

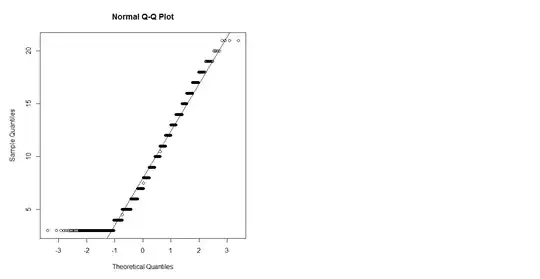
This QQ plot has the following salient features:

1. The stairstep pattern, in which only specific, separated heights ("sample quantiles") are attained, shows the data values are discrete. Almost all are whole numbers from $3$ through $21$. A few half-integers appear. Evidently some form of rounding has occurred.

2. Because the extreme "theoretical quantiles" are at $\pm 3.2$ (roughly), there must be around $1400$ data shown. This is because the extremes for this much Normally distributed data would have Z-scores about $\pm 3.2$. (This estimate of $1400$ is rough, but it's in the right ballpark.)

3. There is a large number of values at the minimum of $3$, far more than any other value. This is characteristic of left censoring, whereby any value less than a threshold ($3$) is replaced by an indicator that it is less than that threshold--and, for plotting purposes, all such values are plotted at the threshold. (For more on what censoring does to probability plots, see the analysis at https://stats.stackexchange.com/a/30749.)

4. Apart from this "spike" at $3$, the rest of the points come fairly close to following the diagonal reference line. This suggests the remaining data are not too far from Normally distributed.

5. A closer look, though, shows the remaining points are initially slightly lower than the reference line (for values between $5$ and $10$) and then slightly greater (for values between $13$ and $20$) before returning to the line at the end (value $21$). This "curvature" indicates a certain form of non-normality.

This particular kind of curvature is consistent with data that are starting to follow an extreme-value distribution. Specifically, consider the following data-generation mechanism:

• Collect $k\ge 1$ independent, identically distributed Normal variates and retain just the largest of them.

• Do that $n = 1400$ times.

• Left-censor the data at a threshold of $3$.

• Record their values to two or three decimal places.

• Round the values to the nearest integer--but don't round any value that is exactly a half-integer (that is, ends in $.500$).

If we set $k=50$ or thereabouts and adjust the mean and standard deviation of those underlying Normal variates to be $\mu = -10$ and $\sigma = 7.5$, we can produce random versions of this QQ plot and most of them are practically indistinguishable from it. (This is an extremely rough estimate; $k$ could be anywhere between $8$ and $200$ or so, and different values of $k$ would have to be matched with different values of $\mu$ and $\sigma$.) Here are the first six such versions I produced:

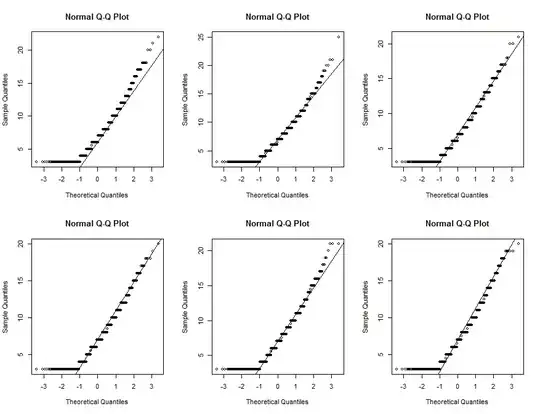
What you do with this interpretation depends on your understanding of the data and what you want to learn from them. I make no claim that the data actually were created in such a way, but only that their distribution is remarkably like this one.

This is R code to reproduce the figure (and generate many more like it if you wish).

k <- 50
mu <- -10
sigma <- 7.5
threshold <- 3
n <- 1400
#
# Round most values to the nearest integer, occasionally
# to a half-integer.
#
rnd <- function(x, prec=300) {
  y <- round(x * prec) / prec
  ifelse(2*y == floor(2*y), y, round(y))
}
q <- c(0.25, 0.95) # Used to draw a reference line
par(mfcol=c(2,3))
set.seed(17)
invisible(replicate(6, {

  # Generate data
  z <- apply(matrix(rnorm(n*k), k), 2, max) # Max-normal distribution
  y <- mu + sigma * z                       # Scale and recenter it
  x <- rnd(pmax(y, threshold))              # Censor and round the values

  # Plot them
  qqnorm(x, cex=0.8)
  m <- median(x)
  s <- diff(quantile(x, q)) / diff(qnorm(q))
  abline(c(m, s))
  #hist(x)    # Histogram of the data
  #qqnorm(y)  # QQ plot of the uncensored, unrounded data
}))

Answer 2

(As Nick Cox also suggests) the distribution is right skew and discrete, but to the right of the spike at 3, is roughly similar to a standard normal truncated below -1 (which is right skew), but with a shorter right tail.

I've made some additional comments on the diagram below:

Here's a frequency plot (a sample pmf) that would yield a Q-Q plot roughly similar to yours:

Answer 3

Your data are positively skewed, meaning skewed to the right. "Right" or "left" is a matter of the longer, more stretched out, tail in the distribution. The terminology presupposes that you are (imagining) looking at a conventional histogram with a horizontal magnitude scale.

But clearly you have integer values between 3 and 21, hence the appearance of an irregular staircase, except that there are values such as 4.5. You have a prominent spike of values at 3: that should not come as a surprise to you, but we can't tell you why. Similarly, if these are counts, then the absence of 0, 1 and 2 may (or may not) be worth comment.

It's possible, however, that numeric measures of skewness may be negative as a side-effect of the spike.

The values are reminiscent of grades on a test in which most students did poorly, but few were utterly abysmal, and some messy answers provoked compromise marks.

Values in the data that are the same must be plotted at the same horizontal level at various levels on the $y$ axis. The average over samples of the same size from a true Gaussian distribution would all be distinct, so the values on the $x$ axis must be distinct.

The spike alone means that you can't call this distribution "normal". If you thought this distribution would be normal, you need to review your thinking.