I am running a Kwiatkowski–Phillips–Schmidt–Shin test (KPSS test) in R (urca::ur.kpss). However, I am quite unsure if it is performed correctly, because the results are the same for each data column.
> dput(datSel)
structure(list(c = c(142.8163942, 143.5711365, 145.3485827, 142.0577145,
139.4326176, 140.1236581, 138.6560282, 136.405036, 133.9337229,
133.8785538, 132.0608441, 130.0866307, 120.1320237, 119.6368882,
114.3312943, 117.5084111, 114.4960017, 112.9124518, 112.8185478,
112.3047916, 106.632639, 106.2107158, 106.8455028, 106.3879556,
104.3451786, 102.9085952, 101.0967783, 101.7858278, 101.0749044,
102.6441976, 102.0666152, 100, 97.14084104, 97.49972913, 96.91453836,
96.05132443, 94.98057971, 92.78373451, 92.67526281, 91.82430571,
91.4153859, 89.51740671, 89.01587176, 84.62259911, 91.48598494,
89.12053042, 90.02364352, 90.92496121, 89.42963565, 91.93886583,
88.83918306, 90.39513509, 87.54571761, 91.3386451, 87.7836994,
91.79178376, 87.56903138, 87.77875755, 89.29938784, 90.88084014
), d = c(17703.7, 17599.8, 17328.2, 17044, 17078.3, 16872.3,
16619.2, 16502.4, 16332.5, 16268.9, 16094.7, 15956.5, 15785.3,
15587.1, 15460.9, 15238.4, 15230.2, 15057.7, 14888.6, 14681.1,
14566.5, 14384.1, 14340.4, 14383.9, 14549.9, 14843, 14813, 14668.4,
14685.3, 14569.7, 14422.3, 14233.2, 14066.4, 13908.5, 13799.8,
13648.9, 13381.6, 13205.4, 12974.1, 12813.7, 12562.2, 12367.7,
12181.4, 11988.4, 11816.8, 11625.1, 11370.7, 11230.1, 11103.8,
11037.1, 10934.8, 10834.4, 10701.3, 10639.5, 10638.4, 10508.1,
10472.3, 10357.4, 10278.3, 10031), e = c(71.0619, 70.9383, 71.162,
71.138, 71.2286, 71.5095, 71.565, 71.3246, 71.4963, 71.3738,
71.4276, 71.3065, 71.0246, 71.3244, 71.0619, 70.9811, 71.2149,
70.8342, 70.5568, 70.5444, 70.3286, 70.179, 70.2555, 70.5103,
70.8038, 70.6748, 70.9769, 70.6988, 70.2125, 70.1661, 69.6284,
69.5613, 68.9837, 68.8606, 68.4223, 67.963, 67.6293, 67.5905,
67.1857, 67.1248, 66.7075, 66.5857, 66.4303, 66.2826, 68.7514,
68.8897, 69.0824, 68.9718, 68.7927, 68.6387, 68.8053, 68.7286,
68.4141, 68.2357, 68.4785, 68.4171, 68.4782, 68.3978, 68.5344,
68.4772), f = c(2160.080078, 2203.939941, 2500.850098, 2523.820068,
2546.54, 2528.449951, 2223.97998, 2352.01001, 2401.21, 2089.73999,
1975.349976, 2159.060059, 1891.68, 1947.849976, 2766.72998, 2882.179932,
2947.24, 2541.629883, 2278.800049, 2634, 2495.56, 2637.280029,
2098.649902, 1696.619995, 1750.83, 2767.76001, 3943.149902, 3765.909912,
4512.98, 4527.299805, 4869.259766, 4645.5, 4463.47, 3868.27002,
3745.719971, 4139.830078, 3667.03, 3457.449951, 3049.909912,
2632.899902, 2431.38, 2042.869995, 1989.400024, 1866.76001, 1545.15,
1351.890015, 1305.709961, 1163.109985, 1150.05, 1070.209961,
1243.069946, 1289.16, 1140.36, 1084.069946, 1206.819946, 1186.540039,
1073.3, 1161.160034, 1129.579956, 1130.069946), g = c(5.7393,
5.7072, 5.6126, 5.6411, 5.5114, 5.4551, 5.1613, 5.4087, 5.0227,
5.2039, 4.9501, 4.5008, 4.9143, 4.1372, 4.5604, 4.7979, 4.5454,
4.8863, 5.0496, 4.9757, 5.4705, 5.8403, 5.4328, 4.6986, 4.4481,
4.1385, 3.8379, 4.2183, 4.5429, 5.03, 5.1821, 4.8269, 5.0469,
5.1054, 5.3959, 5.5413, 5.8139, 5.8611, 5.8396, 5.1964, 5.6386,
5.6615, 5.5751, 5.2251, 4.4682, 4.262, 4.3487, 4.1654, 3.9651,
3.9105, 3.7954, 4.1595, 3.8174, 3.6349, 3.6119, 3.4004, 3.366,
3.3953, 3.3621, 3.9338), h = c(88.548662, 90.58853576, 91.32289522,
91.56290683, 108.4682322, 93.86541244, 100.3414441, 91.98328561,
95.53905246, 102.6461104, 97.9505881, 108.912959, 114.4931447,
108.0431511, 98.58118608, 107.9440773, 99.41777306, 104.868483,
100.3338425, 98.06667712, 100.6353811, 100.6491181, 106.4241282,
79.3180456, 80.40781739, 85.35716451, 102.9110831, 88.99947733,
99.38928861, 87.57579615, 87.49264945, 90.29013182, 92.13878645,
90.15141711, 83.90950016, 97.24552675, 93.38024804, 94.16745797,
98.90106448, 94.73366108, 104.1079291, 98.20132446, 97.70974526,
91.86162897, 101.5381154, 94.56938821, 86.91581151, 87.16428746,
87.35114009, 85.0634706, 86.2179337, 82.34156437, 79.86840987,
84.20717658, 85.29553997, 90.94079268, 92.84823122, 88.90113767,
88.05502443, 92.38787475), i = c(363.81, 361.19, 362.35, 359.09,
359.31, 355.8, 356.64, 353.83, 353.49, 348.92, 348.8, 344.85,
343.48, 340.75, 341.1, 335.72, 331.29, 328.21, 328.95, 325.92,
324.83, 322.83, 323.18, 321.66, 322.94, 323.14, 322.89, 318.34,
315.85, 311.61, 311.3, 308.34, 306.1, 305.64, 305.58, 302.91,
301.64, 300.24, 299.54, 298.58, 296.4, 293.87, 293.35, 291.61,
289.43, 288.03, 287.69, 287.6, 285.95, 284.8, 284.63, 282.62,
281.24, 280, 280.09, 277.65, 275.73, 273.12, 272.78, 272.25),
j = c(307.5, 308.6, 308.9, 309.7, 311.1, 311.6, 311.6, 313.9,
314.9, 314.8, 314.9, 314.5, 313.4, 313, 312.9, 309, 304.5,
302.76, 299.28, 293.44, 291.52, 291.71, 290.61, 294.17, 297.74,
300.02, 295.91, 292.9, 289.23, 287.49, 285.86, 283.84, 281.1,
280.37, 278.63, 275.44, 273.88, 273.24, 274.6, 275.15, 269.77,
267.66, 264.29, 262.27, 260.53, 260.52, 261.54, 263.27, 261.45,
261.81, 261.99, 261.35, 262.64, 264.74, 265.56, 265.47, 267.3,
265.47, 262.64, 260.72), k = c(103.3086091, 102.9085757,
103.6086341, 107.5089591, 107.9089924, 108.9090758, 104.3086924,
97.80815068, 104.8087341, 108.0090008, 103.4086174, 104.5087091,
105.8088174, 100.308359, 102.6085507, 100.4083674, 96.80806734,
99.50829236, 102.708559, 100.7083924, 103.0485874, 103.9186599,
104.7887324, 105.0787566, 103.3386116, 104.0186682, 102.5685474,
112.4193683, 105.8488207, 104.5987166, 107.3989499, 108.6490541,
107.2989416, 106.2388532, 101.3084424, 98.02816901, 102.1785149,
97.83815318, 98.70822569, 88.85740478, 92.66772231, 95.36794733,
91.4076173, 87.54729561, 89.66747229, 87.73731144, 87.34727894,
90.9275773, 78.26652221, 80.29669139, 79.90665889, 77.68647387,
77.59646637, 78.46653888, 77.68647387, 77.01641803, 84.45703809,
77.97649804, 76.72639387, 77.88649054), l = c(109.1, 109.1,
108.8, 108.2, 107.6, 107.2, 107.3, 106.7, 106.4, 106, 105.9,
104.9, 103.8, 103.5, 103, 102.3, 101.3, 100.5, 99.6, 98.6,
97.43314, 96.68301, 95.84954, 95.18276, 94.76602, 94.01589,
92.84903, 91.18208, 89.76517, 89.18174, 88.51496, 87.76484,
86.68132, 85.93119, 85.18107, 84.51429, 83.76416, 83.43077,
83.26407, 82.93068, 82.46215, 82.14979, 81.83744, 81.05654,
80.43183, 80.35374, 80.27565, 79.9633, 79.72903, 79.57285,
79.57285, 79.26049, 79.02623, 79.10432, 79.02623, 78.71387,
78.4796, 78.24534, 77.93298, 77.69871), m = c(108.26667,
107.96667, 107.46667, 106.76667, 106.66667, 106.6, 106.43333,
105.83333, 105, 104.8, 104.46667, 103.46667, 102.4, 102.56667,
102.2, 101.96667, 100.77774, 100.47032, 100.41443, 98.48607,
97.47997, 97.22844, 96.55771, 96.52976, 96.58566, 98.2066,
96.58566, 94.0704, 92.00231, 92.03026, 91.86257, 90.40932,
89.26348, 88.84427, 87.19538, 85.32292, 84.28887, 83.61814,
83.72993, 83.59019, 83.22324, 82.61167, 82.09794, 80.36107,
78.86882, 78.42849, 77.93923, 77.05856, 76.39806, 76.34913,
76.22682, 75.39507, 75.05259, 75.24829, 75.12598, 74.34316,
74.04961, 73.60927, 73.21786, 72.67968), n = c(108.56667,
108.56667, 108.23333, 107.3, 107.13333, 106.8, 106.63333,
105.76667, 105.46667, 105.06667, 104.8, 103.23333, 102.5,
102.6, 102.36667, 102.1, 100.5226, 100.32976, 100.71544,
98.29121, 97.35458, 97.43723, 96.80362, 96.85872, 96.36285,
98.75953, 97.05155, 93.6907, 91.12874, 91.29403, 91.29403,
89.44831, 88.07091, 87.57505, 85.86707, 83.96626, 83.4153,
82.64396, 82.47867, 82.17564, 82.00498, 81.76645, 81.12244,
79.59587, 78.02161, 77.73538, 77.18677, 76.11341, 75.39783,
75.42168, 75.04004, 73.94283, 73.94283, 74.08594, 73.7043,
72.67864, 72.2493, 71.89151, 71.43831, 70.62732), o = c(57844L,
57844L, 57667L, 57168L, 57080L, 56904L, 56813L, 56353L, 56193L,
55980L, 55838L, 55003L, 54612L, 54666L, 54541L, 54398L, 53567L,
53465L, 53670L, 52379L, 51878L, 51923L, 51585L, 51615L, 51351L,
52629L, 51718L, 49927L, 48562L, 48649L, 48640L, 47666L, 46932L,
46668L, 45758L, 44745L, 44428L, 44046L, 43944L, 43779L, 43690L,
43563L, 43219L, 42407L, 41567L, 41416L, 41123L, 40551L, 40170L,
40182L, 39979L, 39395L, 39394L, 39471L, 39267L, 38721L, 38514L,
38309L, 38061L, 37617L), p = c(59373L, 59209L, 58935L, 58551L,
58496L, 58458L, 58368L, 58039L, 57582L, 57472L, 57289L, 56742L,
56156L, 56248L, 56046L, 55919L, 55243L, 55075L, 55045L, 53988L,
53436L, 53298L, 52930L, 52915L, 52947L, 53834L, 52946L, 51567L,
50433L, 50449L, 50357L, 49557L, 48932L, 48671L, 47722L, 46772L,
46213L, 45865L, 45919L, 45826L, 45612L, 45276L, 44994L, 44041L,
43225L, 42983L, 42715L, 42232L, 41870L, 41843L, 41777L, 41321L,
41132L, 41240L, 41172L, 40743L, 40587L, 40352L, 40127L, 39814L
), q = c(96819L, 96819L, 96090L, 94632L, 94632L, 94632L,
93727L, 91917L, 91917L, 91917L, 90779L, 88503L, 88416L, 88416L,
88270L, 87978L, 87996L, 87996L, 87566L, 86706L, 86706L, 86706L,
85794L, 83970L, 83970L, 83970L, 83007L, 81081L, 81081L, 81081L,
80423L, 79107L, 79107L, 79107L, 78321L, 76749L, 76533L, 76533L,
75983L, 74883L, 74883L, 74883L, 74575L, 73959L, 73959L, 73959L,
73167L, 71583L, 71583L, 71583L, 70858L, 69408L, 69408L, 69408L,
68594L, 66966L, 66831L, 66342L, 65853L, 64875L), r = c(144.5,
146.5, 147.3, 143.3, 140.1, 142.8, 141.2, 140.2, 137.8, 137.4,
136.6, 137.6, 125.5, 125.7, 120.5, 124.2, 121.5, 119.8, 121.3,
122, 114.1, 114.4, 114.7, 116.1, 112.8, 111.8, 110.2, 111.7,
112.2, 113.7, 112.7, 110.5, 107, 107.5, 108, 107.1, 106.7,
103.3, 104.2, 104.3, 104.1, 101.3, 100.5, 94.3, 105.6, 101,
102, 103.1, 101.4, 105.5, 100.5, 102.8, 100.5, 105.1, 98.8,
105.1, 98.2, 98.2, 100.6, 103), s = c(132.2, 133.9, 133.5,
126, 125, 122.6, 122.6, 123.8, 124.5, 120.2, 120.2, 123.5,
105.2, 116.4, 111.5, 116.4, 116.1, 114.3, 117, 117.9, 107.1,
104.5, 110.6, 110.5, 104.2, 105.4, 106.2, 110.3, 106.8, 111.4,
111.2, 108.5, 93.5, 101.5, 101.4, 101.3, 101.7, 96.8, 97.3,
100, 97.5, 99.4, 94.8, 93.8, 101.9, 97.4, 97.7, 98.4, 100.6,
100.1, 96.3, 98.1, 93.4, 99.3, 97.3, 99.6, 99.2, 97.8, 100.1,
102.9), t = c(149.8, 151.9, 153.2, 150.7, 146.5, 151.5, 149.2,
147.3, 143.6, 144.8, 143.6, 143.7, 134.1, 129.7, 124.3, 127.5,
123.7, 122.2, 123.1, 123.8, 117.1, 118.6, 116.4, 118.4, 116.4,
114.6, 111.9, 112.2, 114.5, 114.6, 113.4, 111.3, 112.8, 110.1,
110.8, 109.5, 108.8, 106.1, 107.1, 106.1, 107, 102.1, 103,
94.5, 107.2, 102.5, 103.9, 105.1, 101.7, 107.8, 102.4, 104.8,
103.6, 107.6, 99.5, 107.4, 97.8, 98.4, 100.8, 103), u = c(155.2,
157.6, 159, 156.5, 151.4, 155, 152, 149, 146.4, 147.9, 146.6,
146.3, 137.1, 131.1, 124.5, 127.5, 123.1, 121.9, 123, 123.5,
116.4, 117.7, 116.4, 118.1, 116.5, 113.7, 110.2, 111, 113.9,
113.9, 113.6, 110.9, 113.2, 109.9, 111.7, 109.7, 110.1, 106.3,
107.4, 105.9, 107.2, 101.6, 103.8, 94.1, 108.4, 102.7, 104.1,
105.1, 101.5, 108.8, 102.3, 105.4, 103, 107.2, 99.3, 107.6,
97.4, 97.6, 101.2, 103.9), v = c(112.6, 112.7, 113.6, 110.7,
113.4, 127.1, 130.1, 135.7, 123.7, 123.2, 123, 125.5, 113.5,
120.2, 123.3, 128, 128.2, 124.6, 124, 125.8, 122.2, 124.8,
116.6, 120.4, 115.9, 120.6, 124, 120.6, 119, 120.1, 111.6,
114, 110.2, 111.6, 104.5, 107.9, 100.4, 104.7, 105, 106.9,
105.1, 105.8, 97.3, 96.6, 99.1, 101.1, 102.5, 105.2, 103,
101, 102.7, 100.5, 107.4, 110.1, 101.3, 105.7, 100.3, 104.1,
98.4, 97.2)), .Names = c("c", "d", "e", "f", "g", "h", "i",
"j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v"
), row.names = c(NA, -60L), class = "data.frame")
> resKpssT <- lapply(datSel,function(x){ summary(ur.kpss(x,type="tau")) })
> (resKpssT)
$c
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3717
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$d
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1771
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$e
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.158
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$f
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.2767
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$g
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1737
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$h
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.0815
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$i
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.2921
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$j
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1445
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$k
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3354
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$l
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3125
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$m
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1857
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$n
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1818
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$o
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1822
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$p
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1847
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$q
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.0801
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$r
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3628
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$s
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3033
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$t
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3514
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$u
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.3544
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
$v
#######################
# KPSS Unit Root Test #
#######################
Test is of type: tau with 3 lags.
Value of test-statistic is: 0.1649
Critical value for a significance level of:
10pct 5pct 2.5pct 1pct
critical values 0.119 0.146 0.176 0.216
> cv.kpss.tau <- sapply(resKpssT, function(x) x@cval)
> (cv.kpss.tau)
c d e f g h i j k l m n o p q r s t
[1,] 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119 0.119
[2,] 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146 0.146
[3,] 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176 0.176
[4,] 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216 0.216
u v
[1,] 0.119 0.119
[2,] 0.146 0.146
[3,] 0.176 0.176
[4,] 0.216 0.216
You can see that all critical values are the same and they preach the critical values. Hence, all data should be non-stationary.
However, I do not think that this might be correct, because when looking for example at time series, q.
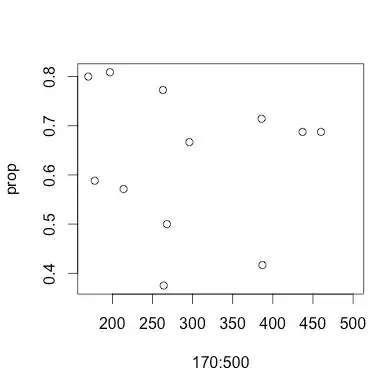
Any suggestion what I am doing wrong?
UPDATE
I created a table of my series for the KPSS test values.
Is this correct?
I also ran my results through a Dick Fuller test, which basically shows me complementary results:
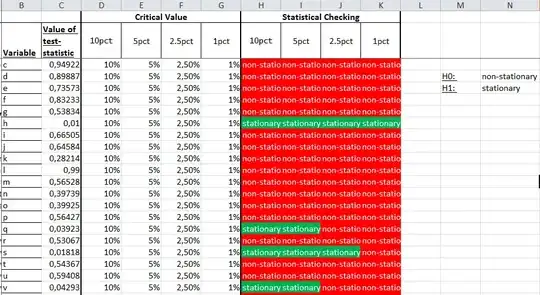
My excel formula is in pseudocode:
=IF("calculated p-value" <= "critical value"; H1 ; H0 )
Here you can find an excel sheet, which I am using for the calculations:
The two pictures show complementary results to me. Hence, I am guessing I am doing sth wrong.
Any recommendation what I am doing wrong?