3

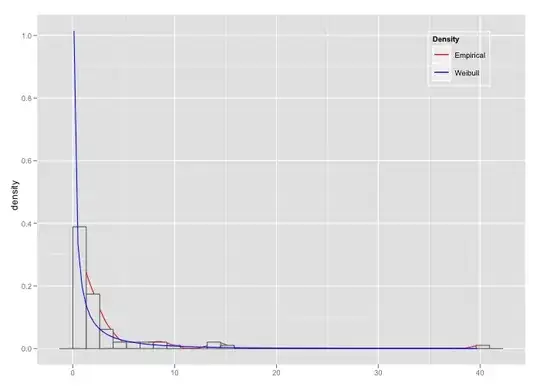
Let's suppose I have a set of measurements on a continuous variable which follows a power law distribution, and I’m interested in deriving the exponent of such a distribution.

So far I've used the binning method, so I was dividing the interval in n bins, plotting the number of observation for each bin in log-log scale and fitting a regression line trough the data. However this way of estimating the exponent is not enough accurate.

Now I’d like to move on and use the maximum likelihood method. But I’m a bit confused, maybe because I keep referring to the binning method. I know how to write the function of the expected theoretical distribution but I can’t visualize how to derive the empirical distribution. Can anyone point me in the right direction?

chl
  • 50,972
  • 18
  • 205
  • 364

4 Answers4

4

I would recommend using the fitdistrplus package, which has better support for maximum likelihood estimation. Read the vignette for more details on how to go about estimating any distribution. Here is an example using a weibull distribution.

# LOAD LIBRARIES 
library(fitdistrplus);
library(ggplot2);

# GENERATE DUMMY DATA 
x1 = rweibull(100, shape = 0.5, scale = 1); 

# ESTIMATE WEIBULL DISTRIBUTION
f1 = fitdist(x1, 'weibull', method = 'mle');

# PLOT HISTOGRAM AND DENSITIES
p0 = qplot(x1[x1 > 0.1], geom = 'blank') +
  geom_line(aes(y = ..density.., colour = 'Empirical'), stat = 'density') +  
  geom_histogram(aes(y = ..density..), fill = 'gray90', colour = 'gray40') +
  geom_line(stat = 'function', fun = dweibull, 
     args = as.list(f1$estimate), aes(colour = 'Weibull')) +
  scale_colour_manual(name = 'Density', values = c('red', 'blue')) + 
  opts(legend.position = c(0.85, 0.85))

enter image description here

Ramnath
  • 151
  • 4
3

For fitting continuous distributions (like exponential) try to use fitdistr() from package MASS (see ?fitdistr or the Ricci's paper as DWin pointed out). It uses maximum likelihood parameter estimation.

You should probably ask at stats.stackexchange.com.

Tomas
  • 5,735
  • 11
  • 52
  • 93
1

http://cran.r-project.org/doc/contrib/Ricci-distributions-en.pdf

DWin
  • 7,005
  • 17
  • 32
0

It is true that most statistical software package come with function implementing the stuff for you however, I always find it useful to understand how the black box works.

So in the case of the MLE for the power law (easy to derive), the best $\alpha$ estimate is

$\hat \alpha = 1+ n\left(\sum_{i=0}^n\ln{x_i/x_{min}}\right)^{-1}$ where $x_{min}$ is the smallest observation you have and $n$ the number of observations.

You can then plot

$y=\frac{1-\hat\alpha}{x_{min}}\left(\frac{x}{x_{min}}\right)^{-\hat\alpha}$

John
  • 735
  • 1
  • 6
  • 9