8

Interpretation of log transformed predictor neatly explains how to interpret a log transformed predictor in OLS. Does the interpretation change if there are 0s in the data and the transformation becomes log(1 + x) instead?

Some authors (e.g. Fox and Weisberg 2011) recommend adding a start (i.e. a positive constant) if a log transformation is necessary to correct skewness and improve symmetry, but the data contains zeros.

Consider a variation of the Ornstein example in CAR (p. 303): 

require(car)
data(Ornstein)
boxplot(Ornstein$interlocks, horizontal = T)

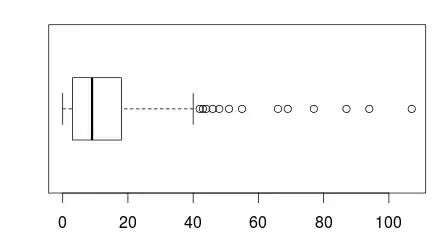
enter image description here

The data is clearly right skewed, and contains 0s. 

summary(powerTransform(1 + Ornstein$interlocks))
## bcPower Transformation to Normality 
## 
##                         Est.Power Std.Err. Wald Lower Bound Wald Upper Bound
## 1 + Ornstein$interlocks    0.1248    0.053           0.0209           0.2287
## 
## Likelihood ratio tests about transformation parameters
##                              LRT df      pval
## LR test, lambda = (0)   5.502335  1 0.0189911
## LR test, lambda = (1) 262.431991  1 0.0000000

The powerTransform() function suggests that a log(1 + x) transformation here could be useful. 

boxplot(log(1 + Ornstein$interlocks), horizontal = T)

enter image description here

As you can see, symmetry is indeed improved.

Question: If this transformed variable were to be included in an OLS regression as an IV, would the coefficient estimates still have the usual interpretation of log transformed variables?

Community
  • 1
landroni
  • 1,003
  • 15
  • 30

1 Answers1

5

It depends, according to Wooldridge (2012) the percentage change interpretations are often closely preserved, except for changes beginning at $y = 0$ (where the percentage change is not defined). Strickly speaking, using $log(1+y)$ and then interpreting the estimates as if the variable were $log(y)$ is acceptable only if the data on y contain relatively few zeros.

Repmat
  • 3,182
  • 1
  • 15
  • 32