I have a vector X of N=900 observations that are best modeled by a global bandwidth Kernel density estimator (parametric models, including dynamic mixture models, turned out not to be good fits):
Now, I want to simulate from this KDE. I know this can be achieved by bootstrapping.
In R, it all comes down to this simple line of code (which is almost pseudo-code): x.sim = mean(X) + { sample(X, replace = TRUE) - mean(X) + bw * rnorm(N) } / sqrt{ 1 + bw^2 * varkern/var(X) } where the smoothed bootstrap with variance correction is implemented and varkern is the variance of the Kernel function selected (e.g., 1 for a Gaussian Kernel).
What we get with 500 repetitions is the following:
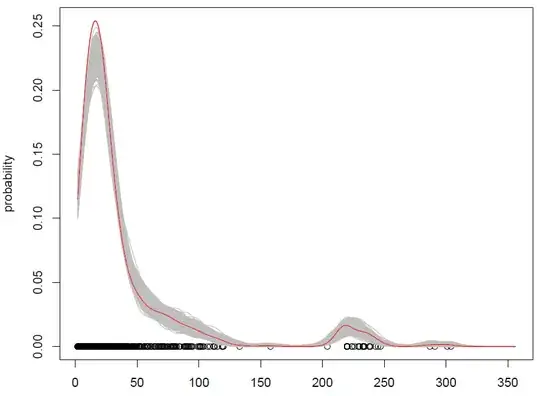
It works, but I have a hard time understanding how shuffling observations (with some added noise) is the same thing as simulating from a probability distribution? (the distribution being here the KDE), like with standard Monte Carlo. Additionally, is bootstrapping the only way to simulate from a KDE?
EDIT: please see my answer below for more information about the smoothed bootstrap with variance correction.