I am not sure whether I am interpreting the cointegration test correctly.
This is the test result:
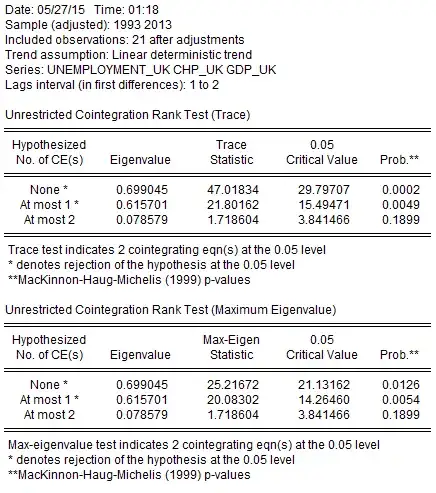
Because of the probability of the test I understand that my series are cointegrated of order 2.
Is that correct?
I am not sure whether I am interpreting the cointegration test correctly.
This is the test result:

Because of the probability of the test I understand that my series are cointegrated of order 2.
Is that correct?
As I read the results, you have two cointegrating equations, or two cointegrating vectors. This translates into cointegration rank being equal to one (number of variables in the system minus the number of cointegrating vectors: $3-2=1$).
Two cointegrating vectors is not the same as cointegration order being equal to two. Your cointegration order is equal to one if each of the original variables is I(1), since there exists a linear combination (actually, two linear combinations -- due to the two cointegrating vectors) of variables that are stationary.
Side note: line 3 Included observations: 21 after adjustments suggests you have very few data points, so the results of the cointegration test may not be reliable.