Suppose I observe a random variable $Y$ for a co-variable $p\in\{70,90,100,...,170\}$.
My goal is create a forecast of $\mathbb{E}(Y)$ for $p\in\{50,70,...,350\}$, i.e., a wider range of $p$ as compared to the observed values of $p$.
Lets assume that $Y\sim Poi\big(\lambda(p)\big)$.
Using this information and a B-Spline (though I could also use just a linear $p$ I'll use a B-Spline to motivate my problem) to fit $\lambda(p)$ I'll get :
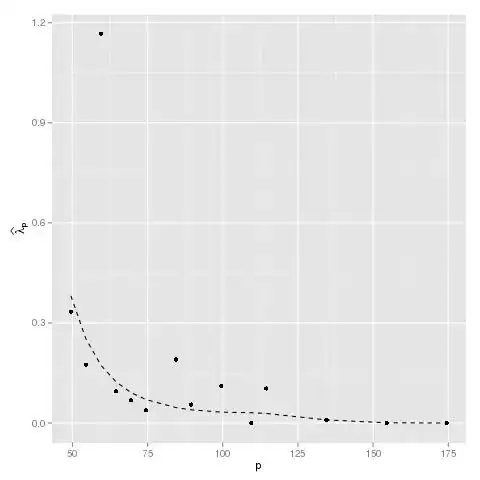
Every point corresponds to the naive ML-Estimator, i.e., equals to $\bar{y}$ for a fixed value of $p$. The dotted curve shows the smoothed version using the B-spline setting.
My question is how do I calculate $\widehat{\lambda}(350)$?
As B-Splines are only defined locally I would use linear extrapolation.
R's gam-function (mgcv-package) calls (if a B-spline is used) the function spline.deswhich calculates derivatives at the boundary knots of the interior knot-interval to calculate the extrapolation.
I did not find any reference which explains how this is done mathematically to get a better inside.