5

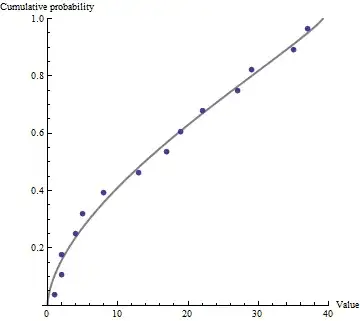
I'm trying to find the estimates for $alpha$ and $beta$ of the beta distribution (red curve) that will fit the black curve (empirical) better.

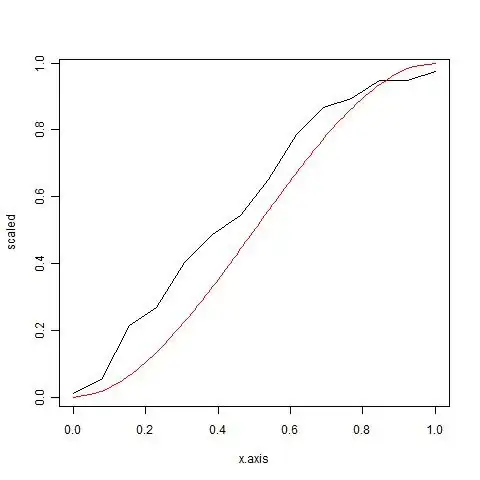
trying to find parameters to make the red curve fit the black curve better

I have a function that finds "non-parametric" inverse cumulative function of my data (boot.mean). I would like to find a distribution that would fit. So far, I think cumulative beta distribution (alpha = beta = 2) could somehow be used. I would love to see a distribution that fits the bill better, though...

# raw data produced by a function (inverse cumulative distribution)
boot.mean <- c(37.021, 35.051, 29.091, 27.094, 22.058, 18.994, 16.944, 12.897, 7.903, 4.926, 3.939, 1.94, 1.94, 0.968)

#"fidge" (not sensu Climategate) boot.mean for comparison to qbeta
scaled <- 1 - (boot.mean/boot.mean[1])
scaled[1] <- 0.01 #dreader zero be gone
range(scaled)
 [1] 0.0100000 0.9738527

# this is the theoretical curve
x <- seq(0, 1, length = 100)
y <- qbeta(x, shape1 = 2, shape2 = 2)

# all along the x axis
x.axis <- seq(from = 0, to = 1, length = length(scaled))

# plot empirical and the theoretical values
plot(x.axis, scaled, type = "l")
lines(y, x, col = "red")

# I'm just an x-con trying to fit a distribution to my data
(beta.fitted <- MASS::fitdistr(x = scaled, densfun = qbeta, start = list(shape1 = 2, shape2 = 2)))
 Error in optim(x = c(0.01, 0.0532130412468599, 0.214202749790659, 0.268145106831258,  : 
   non-finite finite-difference value [2]
 In addition: There were 50 or more warnings (use warnings() to see the first 50)
Roman Luštrik
  • 3,338
  • 3
  • 31
  • 39
  • Just a minor note: I'd rescale with the sum of the values, rather than the first value, if this is a set of counts in disjoint bins (as I inferred in chat). If it's a true CDF, then the maximum value (as you've done) seems reasonable. – Iterator Sep 08 '11 at 13:37

2 Answers2

6

It's not a good idea to rescale the data in this ad hoc way, because it can result in an inferior fit (and ruins any chance of estimating the sampling variance of the scale parameter): just fit a scaled Beta distribution to the data themselves.

You do have to assign percentage points to the data; below I have used $p(i) = (i-1/2)/n$ for the $i^\text{th}$ smallest of $n$ values, sorted as $x_1 \le x_2 \le \cdots \le x_n$. Fit a rescaled CDF to the empirical distribution, $\{(x_i, p_i)\}$. The fit ideally would account for the correlations and heteroscedasticity of the values, but in this case nonlinear least squares does fine:

Data and fitted CDF

This particular fit is $F(x/\gamma)$ where $F$ is the CDF of a Beta($\alpha,\beta$) distribution with $\alpha=0.59$, $\beta=0.87$, and $\gamma=39.2$. This is a U-shaped distribution (i.e., it has modes at both tails). (The correlations and heteroscedasticity indicate that least squares confidence intervals for the parameters cannot be trusted; bootstrap them instead. I haven't carried out the calculation and so will only report the untrustworthy standard errors: they're about $0.06$ for $\alpha$, $0.15$ for $\beta$, and $2.4$ for $\gamma$.)

Consider following this up with a goodness of fit test. Even a simple $\chi^2$ test will give some useful hints about lack of fit. For these data, the graph indicates this fit works pretty well, regardless. A residual-vs.-fit plot suggests the fit is a little better at the high end of the data, but otherwise looks sufficiently random with small residuals:

Residual versus fit plot

This is consistent with a model in which the data have a little bit of measurement error: that would ruin the fit more where the CDF is steep (at the low values) than at other places (the middle to high values).

whuber
  • 281,159
  • 54
  • 637
  • 1,101
  • +1 Good suggestions, especially the note about the measurement error. It occurred to me that the bins at the shortest distances (Roman explained these come from distances) may not be that distinct. It's not uncommon for measurement errors to be larger at tails of sample ranges, especially when binning. – Iterator Sep 08 '11 at 15:33
  • 1
    @Iterator Thanks for the illuminating comments. It would be a little more accurate, and no more computationally difficult, not to bin the data at all. BTW, we don't need the measurement error to be heteroscedastic to explain what's going on: the slope of the fitted CDF suffices. It must be an unusual situation where a beta could be adopted *a priori* as a reasonable model for a set of distances, leading me to suspect that the decent fit here may be an accident. – whuber Sep 08 '11 at 15:38
  • We are in complete agreement. I'm hoping Roman posts a new question about other modeling methods for the raw data. :) – Iterator Sep 08 '11 at 15:40
  • 1
    I forgot to mention that the graphics in the question itself *reverse* the data (as well as rescale them). This explains the visual discrepancy between my rendering of the data values and the original rendering. – whuber Sep 08 '11 at 15:40
2

First remark : your data is nowhere near a distribution, and definitely not the beta function. As I see it, you see your boot.mean as 'density' and your x-axis (the index?) as value. The beta function is limited between 0 and 1, and as the area under the curve of any density function should equal 1, your data doesn't come close. Good point of @whuber: fit a scaled version. Alternatively: Scale to the sum of the data, as @iterator said. Now as the beta function requires scaling twice (both on the X-axis, so the indices and on the Y-axis, being the actual data)

Now you talk about the beta function and you talked about the inverse of the cumulative normal distribution somewhere else. I suppose you mean 'when that distribution is looking in the mirror, it sees what I want to see...' ;-)

So an ad-hoc way of doing this (without any theoretical background, as that background is not the one you need here), is given below. Apart from what everybody else said here, I just want to point out the optim() function, which is doing basically what you're looking for. Regardless whether you fit a scaled and mirrored beta distribution or something that looks close to an inverse normal cumulative distribution for some value of close...

customFit <- function(x, data) {
    d.data <- rev(cumsum(dnorm(1:length(data), x[1], x[2]))) * max(data)
    SS <- sum((d.data - data)^2)
    return(SS)
}

fit.optim <- optim(c(5, 8), customFit, data = boot.mean)

plot(boot.mean)
lines(rev(cumsum(dnorm(1:length(boot.mean), 
         fit.optim$par[1], fit.optim$par[2]))) * max(boot.mean), 
         col = "red")

Note of warning: apart from having a defined function that fits your data, there's little you can do with this result...

Joris Meys
  • 5,475
  • 2
  • 32
  • 43