Lets suppose I have a have a survival curve from 0 to 6000 days using Kaplan -Meier curves. How would I be able to project future survival rates from 6001 and forward ? Is there a function or extrapolation method I can use ?
Below is an example, this is for illustration only:
library(survival)
library(ISwR)
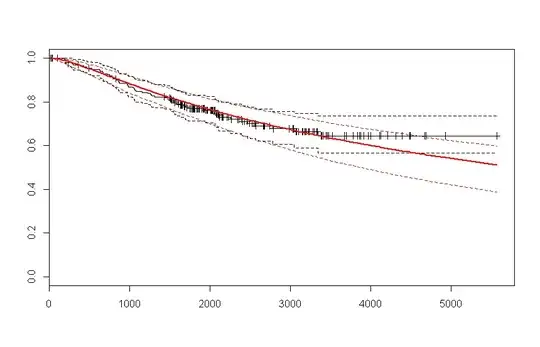
mfit <- survfit(Surv(days, status == 1)~1, data = melanom)
How to project the curves beyond on what is observed below ?
EDIT:
Based on the great response from @CliffAB, I would like to add-on to the question above:
What if we assume its a parametric model (vs. non parametric KM curves) and a distribution, for instance for the same data above, I assome a log normal distribution and run the data, can I use a survival function of the assumed distrubution to project the data ?
require(flexsurv)
parm.curves <- flexsurvreg(Surv(days, status == 1)~1,dist='lnorm',data=melanom)
plot(parm.curves)
The data that I'm working on is more on cutomer retention and it does not behave like the above data. Its just for an illustrative purpose only. But just shows it is difficult to project these type of problems. My question is, can we use assumed distribution survival function to project future survival rates ?
Thanks