44

In linear regression, each predicted value is assumed to have been picked from a normal distribution of possible values. See below.

But why is each predicted value assumed to have come from a normal distribution? How does linear regression use this assumption? What if possible values are not normally distributed?

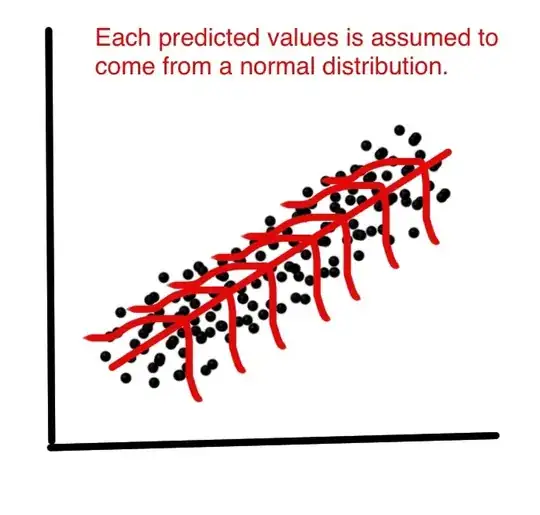
enter image description here

luciano
  • 12,197
  • 30
  • 87
  • 119
  • 3
    Only the errors follow a normal distribution (which implies the conditional probability of Y given X is normal too). This is probably traditional because of reasons relating to the central limit theorem. But you can replace normal with any symmetric probability distribution and get the same estimates of coefficients via least squares. What differs though would be the residual standard error, goodness of fit and the way you validate the assumptions. – Kian Apr 29 '15 at 09:15
  • 4
    Normal assumptions mainly come into inference -- hypothesis testing, CIs, PIs. If you make different assumptions, those will be different, at least in small samples. – Glen_b Apr 29 '15 at 10:20
  • 9
    Incidentally, for ordinary linear regression your diagram should draw the normal curves vertically, not diagonally. – Glen_b Apr 29 '15 at 11:02
  • 1
    @Kian Are you aware of texts or books showing this result? – flow2k Mar 19 '20 at 21:06

5 Answers5

43

Linear regression by itself does not need the normal (gaussian) assumption, the estimators can be calculated (by linear least squares) without any need of such assumption, and makes perfect sense without it.

But then, as statisticians we want to understand some of the properties of this method, answers to questions such as: are the least squares estimators optimal in some sense? or can we do better with some alternative estimators? Then, under the normal distribution of error terms, we can show that this estimators are, indeed, optimal, for instance they are "unbiased of minimum variance", or maximum likelihood. No such thing can be proved without the normal assumption.

Also, if we want to construct (and analyze properties of) confidence intervals or hypothesis tests, then we use the normal assumption. But, we could instead construct confidence intervals by some other means, such as bootstrapping. Then, we do not use the normal assumption, but, alas, without that, it could be we should use some other estimators than the least squares ones, maybe some robust estimators?

In practice, of course, the normal distribution is at most a convenient fiction. So, the really important question is, how close to normality do we need to be to claim to use the results referred to above? That is a much trickier question! Optimality results are not robust, so even a very small deviation from normality might destroy optimality. That is an argument in favour of robust methods. For another tack at that question, see my answer to Why should we use t errors instead of normal errors?

Another relevant question is Why is the normality of residuals "barely important at all" for the purpose of estimating the regression line?

 EDIT

This answer led to a large discussion-in-comments, which again led to my new question: Linear regression: any non-normal distribution giving identity of OLS and MLE? which now finally got (three) answers, giving examples where non-normal distributions lead to least squares estimators.

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
  • Least squares error is equivalent to a normal assumption. – Neil G Apr 29 '15 at 09:04
  • Actually, Florian's answer works for me. If you optimize the parameters to minimize squared error, that is the same is maximizing the log-likelihood of a Gaussian prediction. – Neil G Apr 29 '15 at 09:08
  • Yes, and there is nothing in my answer that contradict that! Maybe I should extend the answer with some more technicalities ... – kjetil b halvorsen Apr 29 '15 at 09:12
  • Maybe I didn't understand your answer, but your first paragraph seems to contradict the equivalence of minimizing squared error and maximizing a normality assumption, or at least it is confusing to me. – Neil G Apr 29 '15 at 09:15
  • 5
    There is no such contradiction. For instance, the Gauss-Markov theorem says that linear least squares is optimal (in least variance sense) among all linear estimators, without any need of distributional assumptions (apart from existing variance). Least squares is a numerical procedure which can be defined independent of any probabilistic model! The probabilistic model is then used to analyze this procedure from a statistical perspective. – kjetil b halvorsen Apr 29 '15 at 09:19
  • The probabilistic model is *equivalent* to least squares. It is only a question of *interpretation*. You cannot have one (least squares minimization) without the other (normality assumption). Similarly, logistic regression is making a Bernoulli assumption, multinomial logistic regression is making a categorical assumption, etc. – Neil G Apr 29 '15 at 10:04
  • No, you are confused! – kjetil b halvorsen Apr 29 '15 at 10:26
  • Why don't you try yourself making a Gaussian model and solving for the maximum likelihood solution; you will find that it is minimizing the squared error. Then go the other way: build a model that minimizes the squared error and verify that this corresponds to a Gaussian model. The two are equivalent. You can also find this result in any machine learning text book. Your first paragraph is clearly wrong. – Neil G Apr 29 '15 at 10:39
  • 3
    @NeilG Certainly MLE for the normal is least squares but that doesn't imply least squares must entail an assumption of normality. On the other hand, large deviations from normality may make least squares a poor choice (when all linear estimators are bad). – Glen_b Sep 19 '15 at 23:29
  • @Glen_b: I see your second statement as tautological with my statement. – Neil G Sep 20 '15 at 14:27
  • 1
    @NeilG What I said there doesn't in any way imply equivalence of LS and normality, but you say explicitly they are equivalent, so I really don't think our two statements are even close to tautological. – Glen_b Sep 20 '15 at 16:11
  • @Glen_b: Going back to my original statement: cross-entropy loss with a normal assumption is equivalent to least squares loss. This is why your statement is true: "large deviations from normality may make least squares a poor choice". Similarly, logistic loss is equivalent to a Bernoulli assumption, multinomial logistic loss to a multinomial assumption, etc. – Neil G Sep 20 '15 at 17:39
  • No, it is not "equivalent to", it can be derived in that way, yes, and that can be very informative, but it (that is, OLS) can also be seen, say, as a purely descriptive statistic. Once a procedure is derived, it can be studied from many different points of view, and is not "equivalent to" any of its derivations. – kjetil b halvorsen Sep 20 '15 at 20:27
  • I disagree: Two models are equivalent if they have the same functional form. What is the benefit to pretending that they are different? The question asker himself says "why is each predicted value assumed to have come from a normal distribution?" and so presumably he is quoting some author who has drawn that connection. – Neil G Sep 20 '15 at 23:58
  • 1
    @Neil Can you show how your statement actually implies what I said? I really don't see it. – Glen_b Sep 21 '15 at 05:43
  • @Glen_b: A problem is defined in terms of a loss function. Given that loss function, various other model choices can be good or bad. If you're going to come up with a loss function, you are deciding how to penalize various errors. Another way to say the same thing is that you are interpreting the model prediction inducing a predictive distribution $P$ over your data. Intuitively, a bad loss function is one that focuses on an arbitrary subset of the data (e.g., outliers if your data has very heavy tails). These points correspond to points that are necessarily surprising given $P$. – Neil G Sep 22 '15 at 00:12
  • 1
    @kjetilbhalvorsen Thanks for the answer; is this topic addressed in any statistical literature/books? – flow2k Mar 19 '20 at 19:37
  • "Then, under the normal distribution of error terms, we can show that this estimators are, indeed, optimal, for instance they are "unbiased of minimum variance", or maximum likelihood. No such thing can be proved without the normal assumption." -- I think this is wrong or at least misleading. OLS is BLUE under Gauss-Markov conditions, which doesn't require normality assumption. – 24n8 Jul 10 '20 at 04:21
  • @lamanon: OK, but BLUE is a very weak optimality---only among **linear estimators**, and might cover situations where no linear estimators are good. – kjetil b halvorsen Jul 17 '20 at 01:28
  • So, unbiased of minimum variance can be proven if we only assume that the error terms are normally distributed ? – seralouk Jan 31 '21 at 09:07
  • @seralouk: It is usually proved on that assumption, yes, but that does not itself preclude that some other assumptions could lead to the same conclusion (but if there are any? I do not know) – kjetil b halvorsen Oct 05 '21 at 03:58
4

This discussionWhat if residuals are normally distributed, but y is not? has well addressed this question.

In short, for a regression problem, we only assume that the response is normal conditioned on the value of x. It is not necessary that the independent or response variables are independent.

Community
  • 1
enaJ
  • 567
  • 1
  • 6
  • 11
3
  1. But why is each predicted value assumed to have come from a normal distribution?

There is no deep reason for it, and you are free to change the distributional assumptions, moving to GLMs, or to robust regression. The LM (normal distribution) is popular because its easy to calculate, quite stable and residuals are in practice often more or less normal.

  1. How does linear regression use this assumption?

As any regression, the linear model (=regression with normal error) searches for the parameters that optimize the likelihood for the given distributional assumption. See here for an example of an explicit calculation of the likelihood for a linear model. If you take the log likelihood of a linear model, it turns out to be proportional to the sum of squares, and the optimization of that can be calculated quite conveniently.

  1. What if possible values are not normally distributed?

If you want to fit a model with different distributions, the next textbook steps would be generalized linear models (GLM), which offer different distributions, or general linear models, which are still normal, but relax independence. Many other options are possible. If you just want to reduce the effect of outliers, you could for example consider robust regression.

Neil G
  • 13,633
  • 3
  • 41
  • 84
Florian Hartig
  • 6,499
  • 22
  • 36
1

Let me stick to the case of a one variable regression. The details are the same, but the notation is more cumbersome in the case of a multivariate regression. Given any data set $(x_i,y_i)$ one can find the 'least squares line' $ y = \beta x +c$ , that is find $\beta$ so that $\sum_i (y_i - \sum_i \beta x_i - c)^2$ is minimized. That is pure mathematics. However under the assumption that the residuals $ \eta_i = y_i - (\beta x_i +c) $ are independent identically distributed gaussian variables with a common variance, then one can get statistical estimates of how accurate the point estimate $\beta$. In particular, one can construct the 95% confidence interval for $\beta$. After all we are assuming that we are sampling from the underlying (true) distribuion and hence if we sampled again, we should expect to get a, possibly just slightly, different answer. In particular, the p-value is the probability of observing the given $\beta$ under the hypothesis that the true value of $\beta$ is zero. So the statistics comes about as information about how accurate is the point estimate $\beta$ . What to do in the case one doesn't have statistical properties of the error term ? With apologies to "The Graduate" - one word bootstrap.

meh
  • 1,902
  • 13
  • 18
  • can you pleas explain what this line means "one can get statistical estimates of how accurate the point estimate β. In particular, one can construct the 95% confidence interval for β." in simple terms ? – star Feb 14 '21 at 17:06
0

After review the question again, I think there is no reason to use the normal distribution unless you want to perform some kind of inference about the parameter of regression. And you can apply linear regression and ignore the distribution of noise term.

Yu Zhang
  • 186
  • 5