7

My particular task is to show $|Y_i-B_0-B_1X_{i}-B_2X_{i}^2 |$ has more than one min value.
We are given $x_1=1$, $x_2=2$, $y_1=3$ and $y_2=4$.

I am truly lost, I need to show there are more than one - manually. I couldn't find any examples to try to grasp this.

user2941942
  • 73
  • 4
  • This reads like routine bookwork, such as might be set as an exercise. Please add the `self-study` tag, read its [tag wiki](http://stats.stackexchange.com/tags/self-study/info) and modify your question as discussed there -- which is to say you need to show what you've actually attempted and where you struck difficulties. – Glen_b Apr 27 '15 at 00:48
  • 2
    One problem you have here is that you only have two data points to determine 3 parameters, so your problem is underdetermined in any case (there's an infinite number of least squares solutions, making the particular issue with least absolute values even when there are more data points than parameters less obvious). Please check the details of your question carefully. – Glen_b Apr 27 '15 at 00:50
  • Yeah, this is all it's written. But I only need to show that there are at least 2 minimal values for this exercise, maybe that makes it doable. I put a lot of thought in this. Looked into transforming into LP problem, but I just got stuck and I can't understand it. – user2941942 Apr 27 '15 at 00:54
  • 1
    It's *doable* alright, pretty trivially so, but unless there's at least 3 points it's pointless, since it doesn't demonstrate much of interest. – Glen_b Apr 27 '15 at 00:57
  • I don't believe you can have made a serious attempt or the point I'm making would be totally obvious. What did you try so far? Did you even plot the points? Plot them! Did you think about what the function is you're fitting? Can you draw a rough one by hand? Can you draw a second? – Glen_b Apr 27 '15 at 01:02
  • @Glen_b I am pretty bad when it comes to absolutes. I drew a line between (1,3) and (2,4). So my initial thoughts are that B0 should be less than three. Maybe I am just overthinking everything – user2941942 Apr 27 '15 at 01:07
  • @Glen_b Also it looks like a linear function so that would make B_2=0 and B_1=1/2 , B_0=3. That would satisfy both and would pass both points. But where do absolutes comes in? It can't be so trivial. You want to tell me, best approach is to nulify one of B1 or B2 and just solve the system of equations to show there are multiple min values? – user2941942 Apr 27 '15 at 01:17
  • You have a solution with B2=0. Choose literally *any* other value for B2 and solve. This has nothing to do with least absolute values, since the same issue occurs with least squares. – Glen_b Apr 27 '15 at 01:48
  • No, the minimal solution will have all residuals 0. Just because you find two solutions that have the same value for $S=\sum_i|Y_i-B_0-B_1X_{i}-B_2X_{i}^2 |$ doesn't mean they're both minima. – Glen_b Apr 27 '15 at 01:49

1 Answers1

11

So that this has some form of answer, let's look at what the OP has discovered, and then put some additional clarity/detail into that (I'm going to go into more detail than I normally would for a self-study question because of the issues with the question, which I think require some explanation):

The issue here is that with 3 parameters and two points the system is underdetermined.

Plotting the points immediately suggests that one can get a perfect fit with a straight line ($B_2=0$).

Simply looking at the plot, and the fact that we're fitting a quadratic through two poiints tells us that a second perfect fit is trivial - choose any $B_2$ and solve for the remaining values.

enter image description here

This non-uniqueness doesn't have anything to do with the non-uniqueness of least absolute values regression, since it works just as well with least squares or many other criteria where a perfect fit yields a minimum. As mentioned, this is simply due to the system being underdetermined. [As a result, this strikes me as a poor example for illustrating anything in particular about least absolute values regression.]

To see nonuniqueness of a least absolute values regression that isn't simply due to the system being underdetermined (i.e. where least squares would also have a non-uniqueness problem), you'd need more data values.

For example, consider fitting a straight line the following data:

x 0 1 2 3
y 0 2 3 3

Here, any line with the minimum value for $S=\sum_i|Y_i-B_0-B_1X_{i}|$ doesn't go through all the data points, but there's still a region of values that attains the minimum value for $S$ (deep blue region outlined in gray); larger values of S are less blue/redder:

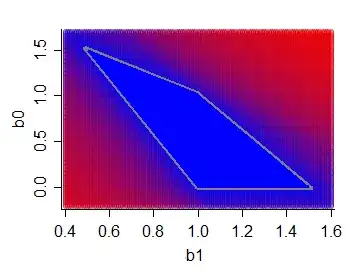
enter image description here

Here are 4 of the lines, each corresponding to points in that optimal parameter region above:

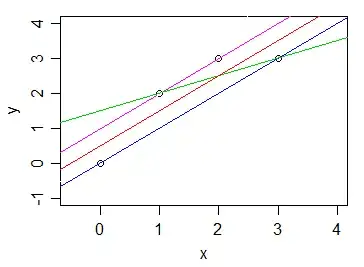
enter image description here

All except the red one are points on the marked boundary in the first plot; the red one is an interior point inside the marked blue region in that first plot.

The red one is also least squares. It's an interior point in the (b1,b0) plot. The other three lines are corner points. If you imagine placing four (thin) poles at the indicated points in the (x,y) plot (sticking out in the z-direction, out of the screen), and pull a string taut close to the red line, then wiggle the string about within the constraints of the four poles, you're wandering about the optimal region.

There's a related example with additional explanation for an intercept-only L1 model here

Glen_b
  • 257,508
  • 32
  • 553
  • 939