7

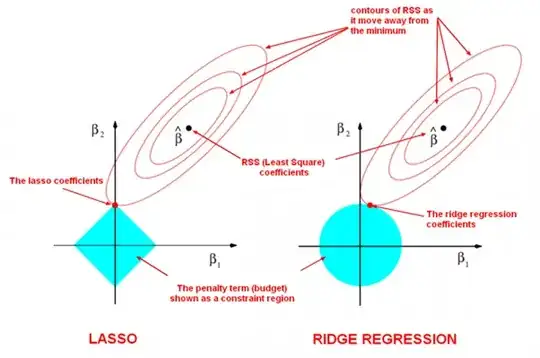
I have found the following image (or a similar version) in a lot of books related to penalized linear models. I get the insight of this image. The ellipsoids are the solution of the linear regression model as the $\beta$ moves away from the minimum, and the blue areas are the constriants of the penalization, so the solution will be the first point in which the red ellipsoids touch the blue area. My question is: Is there any similar geometrical interpretation for the L1 regression (or the general version, quantile regression)? My intuition sugggests that L1 regression may be a polyhedral, but I am not sure and I have not found anything about this in the books

enter image description here

Álvaro Méndez Civieta
  • 1,224
  • 7
  • 16
  • 1
    By L1 regression, are you referring to regression problems where a solution is sought to minimize L1 loss, i.e. $\min_\beta |X\beta - y|$ the absolute differences? – Sycorax May 20 '18 at 17:38
  • 3
    You are confusing the penalty function with the objective function. The penalty is added to the objective. For quantile regression, the objective function is L1 and that is only when estimating the median. Quantile regression is usually unpenalized. – Frank Harrell May 20 '18 at 17:41
  • Yeah, I mean that, working on the mean absolute difference instead of the L2 norm @Sycorax. – Álvaro Méndez Civieta May 20 '18 at 18:23
  • 1
    @FrankHarrell with quantile regression the objective function is a weigthed L1 norm so it can estimate not just the median but any quantile. I know that the penalization is added to that objective function, and that the penalization can be, among other things, L2 norm like ridge regression, or L1 norm like LASSO. But that is not my question. My question is if there is a geometrical interpretation for this quantile regression just as the ellipsoids are the interpretation for OLS. – Álvaro Méndez Civieta May 21 '18 at 04:16
  • The penalizations - the blue part of your diagram - will be absent; the corresponding LS regression won't have them either. The level sets of the L1 norm are generally convex polygons/polyhedrons in parameter space (but you can get degenerate cases). Example contours for a [simple L1 regression](https://stats.stackexchange.com/a/148441/805) (i.e. where the parameter space is the slope and intercept) is [here](https://i.stack.imgur.com/za6Yy.png). In your diagrams the data are centered (so intercept is 0) and there are two predictors but the situation will be similar. – Glen_b May 21 '18 at 07:42
  • Good points @ÁlvaroMéndezCivieta. Technical detail: a weighted L1 norm is not 'officially' an L1 norm. – Frank Harrell May 21 '18 at 11:26

0 Answers0