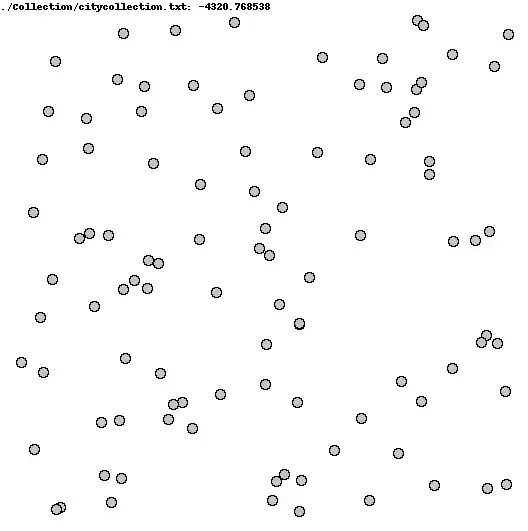
I'm looking for a way to quantify how "clumped" vs homogeneously/uniformly distributed points are in a graph. Each collection has 100 points as (x,y) pairs.
I've attached two graphs as an example. The top one (I think) is visibly more clumped than the bottom one.