Interpreting linear regression residual plots using R

Question

I'm investigating whether there is a relationship between the day of the week and an outcome value using linear regression in R, and would like to understand how to interpret the residual plots.

Data

Example dummy data (the mean and SD are based on actual data I have):

set.seed(14)
mon <- data.frame(id=seq(6, 60*7, by=7), value = rnorm(60, 4372, 145))
tue <- data.frame(id=seq(7, 60*7, by=7), value = rnorm(60, 4433, 206))
wed <- data.frame(id=seq(1, 60*7, by=7), value = rnorm(60, 4671, 143))
thu <- data.frame(id=seq(2, 60*7, by=7), value = rnorm(60, 4555, 154))
fri <- data.frame(id=seq(3, 60*7, by=7), value = rnorm(60, 4268, 149))
sat <- data.frame(id=seq(4, 60*7, by=7), value = rnorm(60, 1579, 110))
sun <- data.frame(id=seq(5, 60*7, by=7), value = rnorm(60, 1136, 68))
startdate <- seq.Date(as.Date("2014-01-01"), by="day", length.out=(60*7) )
id <- seq(1, 60*7)
wd <- weekdays(startdate)
df <- data.frame(id, startdate, wd)
days <- rbind(mon, tue, wed, thu, fri, sat, sun)
df <- merge(df, days)

head(df)
  id  startdate        wd    value
1  1 2014-01-01 Wednesday 4593.117
2  2 2014-01-02  Thursday 4686.159
3  3 2014-01-03    Friday 4352.982
4  4 2014-01-04  Saturday 1825.172
5  5 2014-01-05    Sunday 1206.759
6  6 2014-01-06    Monday 4276.032

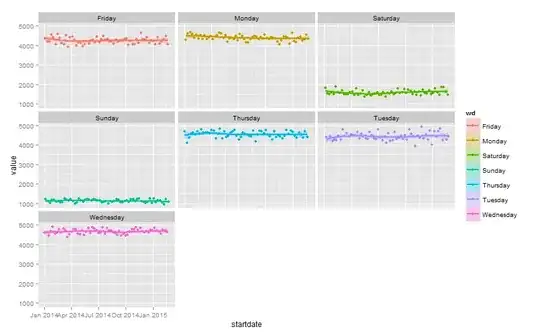
which looks like

library(ggplot2)
ggplot(data=df, aes(x=startdate, y=value, colour=wd)) +
  geom_point() +
  geom_smooth( alpha=.3, size=1, aes(fill=wd)) +
  facet_wrap(~wd) 

Model

Modelling the data using fit <- lm(data=df, value ~ wd) produces the coefficients:

summary(fit)
....
Coefficients:
             Estimate Std. Error  t value Pr(>|t|)    
(Intercept)  4242.60      18.83  225.319  < 2e-16 ***
wdMonday      148.93      26.63    5.593 4.07e-08 ***
wdSaturday  -2661.93      26.63  -99.965  < 2e-16 ***
wdSunday    -3113.78      26.63 -116.933  < 2e-16 ***
wdThursday    299.65      26.63   11.253  < 2e-16 ***
wdTuesday     189.04      26.63    7.099 5.51e-12 ***
wdWednesday   412.52      26.63   15.492  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 145.9 on 413 degrees of freedom
Multiple R-squared:  0.9896,    Adjusted R-squared:  0.9894 
F-statistic:  6539 on 6 and 413 DF,  p-value: < 2.2e-16

The plot of the data, and the coefficients seem to suggests there is a relationship between day of the week and the outcome value.

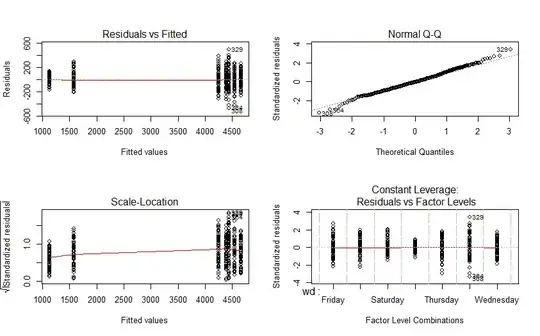
However, I know I also need to consider the residual plots when interpreting the validity of a model. For this example the residual plots are:

par(mfrow=c(2,2))
plot(fit)

Question

Through various stats courses/uni/research (e.g. this question) I know that for a good linear model you are looking for unbiased homoscedastic residuals. But my knowledge on this subject is a bit rusty. Therefore, do my residuals suggest a linear model is not an appropriate fit for the data? And/or is there another aspect to this that I should be considering, or have I completely missed the point all together?

Answer 1

Judging from your diagnostic plots I wouldn't worry about heteroscedasticity and use this model.

However, you can test if modelling the variance of residuals would improve the model:

library(nlme)
fit1 <- gls(value ~ wd, data=df)

fit2 <- gls(value ~ wd, data=df, weights = varIdent(form = ~ 1 | wd))


anova(fit1, fit2)

#     Model df      AIC      BIC    logLik   Test  L.Ratio p-value
#fit1     1  8 5332.321 5364.509 -2658.160                        
#fit2     2 14 5286.911 5343.239 -2629.456 1 vs 2 57.41009  <.0001

As you see, the model, which includes variance parameters, seems slightly better. However, the standard errors or t-values are only slightly different from your original model and you wouldn't infer different conclusions:

summary(fit2)
#Generalized least squares fit by REML
#  Model: value ~ wd 
#  Data: df 
#       AIC      BIC    logLik
#  5286.911 5343.239 -2629.455
#
#Variance function:
# Structure: Different standard deviations per stratum
# Formula: ~1 | wd 
# Parameter estimates:
#Wednesday  Thursday    Friday  Saturday    Sunday    Monday   Tuesday 
#1.0000000 1.2789517 1.2876130 0.9901914 0.5975224 1.1128592 1.5904740 
#
#Coefficients:
#                Value Std.Error    t-value p-value
#(Intercept)  4242.602  20.92298  202.77237       0
#wdMonday      148.931  27.65462    5.38538       0
#wdSaturday  -2661.925  26.39433 -100.85215       0
#wdSunday    -3113.783  23.06607 -134.99409       0
#wdThursday    299.647  29.49021   10.16091       0
#wdTuesday     189.044  33.25205    5.68520       0
#wdWednesday   412.524  26.49180   15.57175       0

anova(fit)
#Analysis of Variance Table
#
#Response: value
#           Df    Sum Sq   Mean Sq F value    Pr(>F)    
#wd          6 834554455 139092409  6538.6 < 2.2e-16 ***
#Residuals 413   8785585     21273 

anova(fit2)
#Denom. DF: 413 
#            numDF  F-value p-value
#(Intercept)     1 210610.5  <.0001
#wd              6  11982.3  <.0001

You could model the weekdays as an ordered factor, which would cause the regression functions to use polynomial contrasts.