I’ve got a question concerning the R package strucchange that I use for testing and dating structural breaks in my PhD thesis. To be specific, I use the generalized fluctuation test framework with CUSUM/MOSUM and in particular Moving Estimates (ME) tests for my analysis. Thus, the following description focuses on the ME test, but in principle is more general to all fluctuation tests.
The problem: I am testing time series data for structural breaks with the ME test that draws on the function efp provided by strucchange. Given the nature of time series data, I want to tackle potential heteroskedasticity and autocorrelation in the data. Strucchange provides some functionality with respect to calculating heteroskedasticity (HC) and autocorrelation (HAC) consistent covariance matrices, e.g., the approaches suggested by Newey-West (1987) or Andrews (1991).
However, this functionality in strucchange is limited to the function gefp that calculates Generalized Empirical M-Fluctuation Processes that as far as I know does not allow to perform estimates-based tests such as the ME test. Thus, I cannot use efp to estimate ME tests (or other tests that are available in this function) using HAC covariance matrices.
The question: Does anybody know how I could make use of the efp function in strucchange for testing and dating structural changes but use HAC covariance matrices to take heteroskedasticity and autocorrelation into account? Maybe there is some way to use the sandwich package for this?
Many thanks for any help!
Here is a minimal working example to show the problem
library(foreign)
library(strucchange)
data("Nile")
#using the function efp to perform a moving estimates test
#assuming sperical disturbances
ocus.nile <- efp(Nile ~ 1, type = "ME")
sctest(ocus.nile)
#applying the vcov function with the kernHAC option to take heteroskedasticity and autocorrelation does not work, i.e., the option is not used and the result is the same
sctest(ocus.nile, vcov=kernHAC)
#using the function gefp to perform a generalized M-fluctuation process however works with vcov
#assuming spherical disturbances
ocus.nile2 <- gefp(Nile ~ 1, fit = lm)
sctest(ocus.nile2)
#controlling for heteroskedasticity and autocorrelation using an appropriate covariance matrix changes the result, i.e. works
ocus.nile2 <- gefp(Nile ~ 1, fit = lm, vcov= kernHAC)
sctest(ocus.nile2)
Some background
Though probably not necessary, here is some more in-depth background about the problem for the interested reader (and the archive). The formulas are taken from Zeileis et al., 2005, ”Monitoring structural change in dynamic econometric models”.
The ME test is used to detect structural breaks in the standard linear regression model over time. What it does it in essence partitioning the data and rather than estimating the regression based on the whole sample, it sequentially moves “through” time in a fixed-width windows containing only a sub-sample of the observations and in each window it estimates the model. These estimates are used to the computation of empirical fluctuation processes that capture fluctuations in regression coefficients and residuals over time. Significant fluctuations of the coefficients are signs of a structural break in the regression. The test statistic of the Moving estimates test is
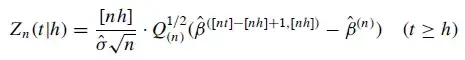
where n is the number of observations, h is the bandwith (how many percent of the total number of observations are used for the window), nh is thus the size of the window, Q_(n)=X_(n)^T X_(N)/n, i=[k+t(n-k)], and sigma^2 is an estimate of the variance. The way I understand the above statistic is that it compares the difference between the sub-sample estimate of beta with the whole sample (the window) estimate and how this difference develops over time. A zero difference would indicate a sub-sample estimate that perfectly equals the whole-sample estimate, which would indicate perfect stability of the coefficient. In my understanding, the efp function in strucchange calculates sigma^2 based on the standard OLS residuals u^ i.e., sigma^2=(1/n-k)∑_(i=1)^n u_i^2 . Thus, in the presence of heteroskedasticity or autocorrelation, the OLS assumption of spherical disturbances will be violated. Thus, ideally, sigma^2 should be estimated based on a HAC covariance matrix to avoid wrong inference.
The question that comes to my mind is whether there is a way to use the ME test based on a HAC estimate. If not, it seems to me that it is limited to spherical disturbances of residuals, which seems to be violated in most applications.