1

I have to solve a problem using a linear mixed model (lmer). Six subjects performed two tests, (test1, test2) in two different locations (on holiday, at work). These are my data:

subj     <- c(1,1,2,2,3,3,4,4,5,5,6,6)
location <- c("holiday","holiday","holiday","holiday","holiday","holiday", 
              "work","work","work","work","work","work")
test     <- c("test1", "test2","test1", "test2","test1", "test2","test1", 
              "test2","test1", "test2","test1", "test2") 
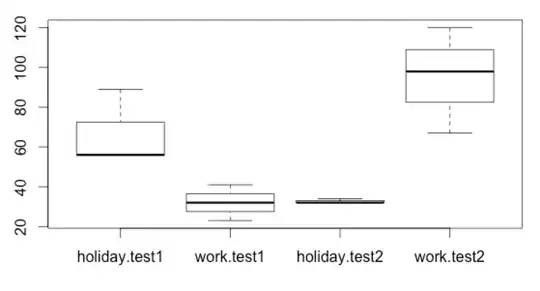
value    <- c(56,32,89,32,56,34,23,98,32,120,41,67)
data     <- data.frame(subj, location, test, value)

Using lmer, I have to verify if there is an effect of the variable location, if there is an effect of the variable test, and if there is an interaction, location X test.

I thought a model like this might be appropriate:

lmer(value ~ location*test + (1|subj))

Could it work?

Furthermore, I have to verify if there is a difference between holiday.test1 and work.test1, and between holiday.test2 and work.test2. I also need p-values.

boxplot(value ~ location*test)

Beta
  • 5,784
  • 9
  • 33
  • 44
Daryl
  • 11
  • 1
  • *It could work* but I think your dataset having essentially two data-points per subject, is too small to estimate robust standard deviations for your random effects. I think simply using a `lm` would greatly simplify your life and provide you with the same inferential insights. Finally giving the really small dataset you are having I wouldn't trust asymptotic tests for $p$-values. I would strongly suggest using `lme4`'s native `bootMer()` function to bootstrap your model and get parametric bootstrap estimates (If you really want a LME model that is). – usεr11852 Mar 31 '15 at 05:44
  • What about creating two models:
    `fm1 = lmer(value ~ test*location + (1|sub), data=tot)` and `fm2 = lmer(value ~ test+location + (1|sub), data=tot)` and using an `anova(fm1,fm2)`. In this case I could say: there is(or not) an interaction `test X location`. Then I could creating two models:`fm3 = lmer(value ~ test+location + (1|sub), data=tot)` and `fm4 = lmer(value ~ test + (1|sub), data=tot)` and verify if `location` affects value... it's correct? I'm a bit confused:)     – Daryl Mar 31 '15 at 11:52
  • I think you are describing backwards elimination here... This is OK given you understand some important caveats about data-dredging (which is a bad thing - see [here](http://stats.stackexchange.com/questions/20836/algorithms-for-automatic-model-selection) :) What I said in my earlier comment still applies. 1. Get more data, or get a simpler model. 2. Use bootstrap to get your $p$-values. Asymptotic tests work for large samples and you appear not to have one. – usεr11852 Mar 31 '15 at 18:08

0 Answers0