I'm trying to determine the optimal reorder point for some products. The reorder point must be greater than the demand during lead time a $\%$ of the times that I should determine, let's say $95\%$.
Problem is demand is of course stochastic. I have made forecasts using Holt/HW Methods, so I have a mean value $\mathbf{D}$ and then I can check the daily error of that demand on passed events. Giving a distribution of that mean's error of that as this:
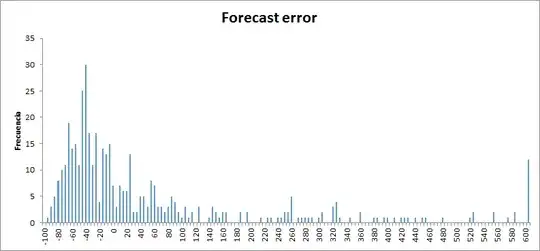
Then I have lead time, distributed for example as this:
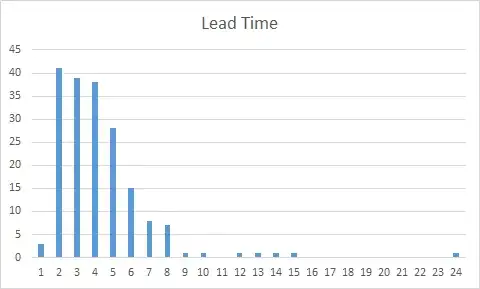
There's a well-known formula that assumes that both distributions are normal, and thus the reorder point can be easily calculated by using the inverse cumulative distribution:
$$ROP = D\cdot LT + Z(CS)\cdot \sqrt{LT\cdot \sigma_{\text{demand}}^2 + D^2\cdot \sigma_{\text{lead time}}^2}$$ Being $CS$ that $95\%$, $Z$ is the inverse cumulative distribution and $\sigma$ the standard deviation.
But these distributions doesn't seem normal at all, so given that I have the historic data, how could I estimate an aproppiate reorder point for that goal of $95\%$ of times being greater than demand during lead time.