15

I am trying to use the 'density' function in R to do kernel density estimates. I am having some difficulty interpreting the results and comparing various datasets as it seems the area under the curve is not necessarily 1. For any probability density function (pdf) $\phi(x)$, we need to have the area $\int_{-\infty}^\infty \phi(x) dx = 1$. I am assuming that the kernel density estimate reports the pdf. I am using integrate.xy from sfsmisc to estimate the area under the curve.

> # generate some data
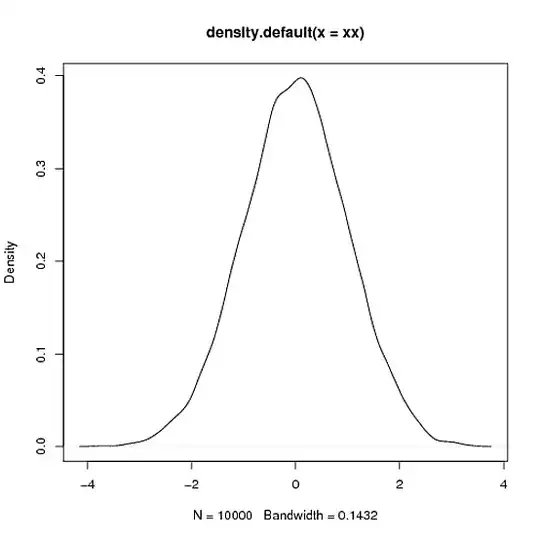
> xx<-rnorm(10000)
> # get density
> xy <- density(xx)
> # plot it
> plot(xy)

plot of the density

> # load the library
> library(sfsmisc)
> integrate.xy(xy$x,xy$y)
[1] 1.000978
> # fair enough, area close to 1
> # use another bw
> xy <- density(xx,bw=.001)
> plot(xy)

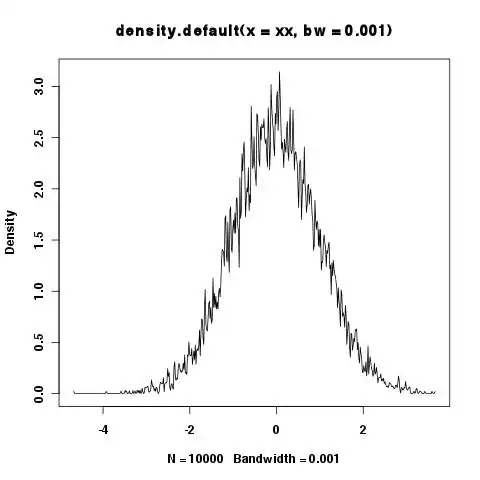
density with bw= .001

> integrate.xy(xy$x,xy$y)
[1] 6.518703
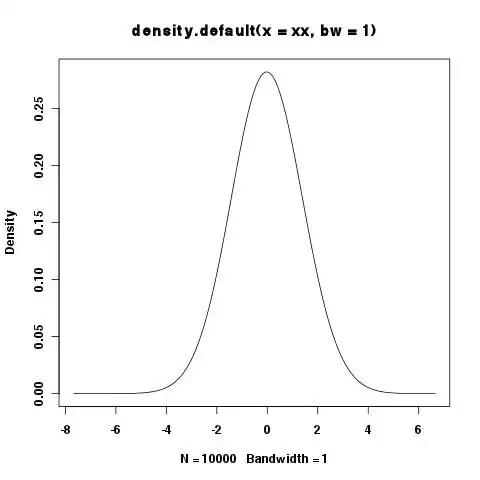
> xy <- density(xx,bw=1)
> integrate.xy(xy$x,xy$y)
[1] 1.000977
> plot(xy)

density with bw = 1

> xy <- density(xx,bw=1e-6)
> integrate.xy(xy$x,xy$y)
[1] 6507.451
> plot(xy)

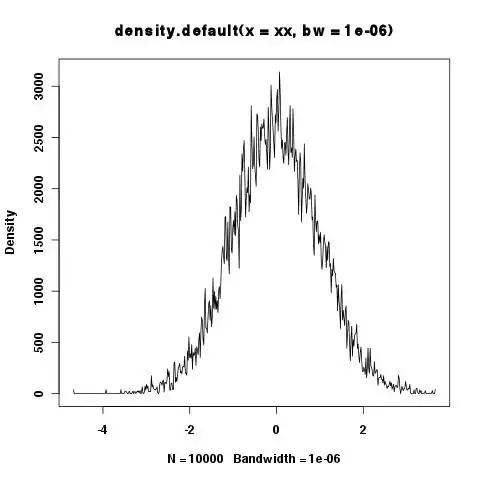
density with bw=1e-6

Shouldn't the area under the curve always be 1? It seems small bandwidths are a problem, but sometimes you want to show the details etc. in the tails and small bandwidths are needed.

Update/Answer:

It seems that the answer below about the overestimation in convex regions is correct as increasing the number of integration points seems to lessen the problem (I didn't try to use more than $2^{20}$ points.)

> xy <- density(xx,n=2^15,bw=.001)
> plot(xy)

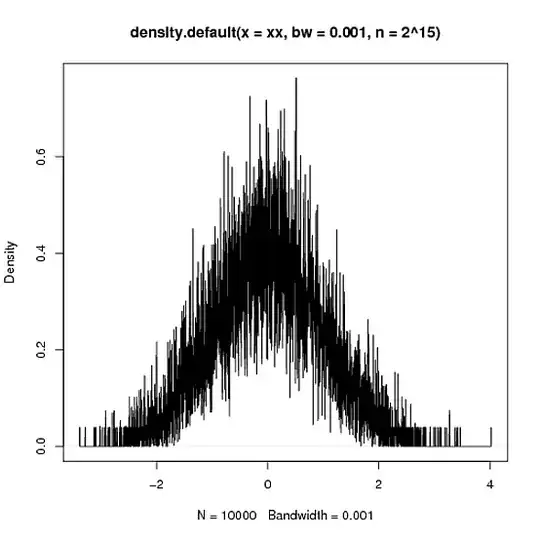
density with higher number of points to sample at

> integrate.xy(xy$x,xy$y)
[1] 1.000015
> xy <- density(xx,n=2^20,bw=1e-6)
> integrate.xy(xy$x,xy$y)
[1] 2.812398
highBandWidth
  • 2,092
  • 2
  • 21
  • 34
  • 3
    This looks like a floating point limitation in density(): in using a bandwidth of 1e-6, you are creating (in theory) a collection of 10,000 spikes, each of total mass 1/10000. Those spikes end up being represented primarily by their peaks, without the gaps being adequately characterized. You're merely pushing density() beyond its limits. – whuber Aug 10 '11 at 01:58
  • @whuber, by floating point limitation, do you mean limits of the precision, as in using floats would lead to greater overestimation of the error compared to using doubles. I don't think I see how that would happen but would like to see some evidence. – highBandWidth Aug 10 '11 at 14:02
  • Your update demonstrates that convexity is *not* the issue; the issue lies in using too small a value of $n$ in the density calculation. – whuber Aug 10 '11 at 15:04
  • Shouldn't the integral value of a *proper* density estimate be $1$? – Has QUIT--Anony-Mousse Sep 17 '13 at 13:18
  • @Anony-Mousse, yes, that is what this question is asking. Why is it not evaluating to 1? – highBandWidth Sep 18 '13 at 20:26

2 Answers2

10

Think about the trapezoid rule integrate.xy() uses. For the normal distribution, it will underestimate the area under the curve in the interval (-1,1) where the density is concave (and hence the linear interpolation is below the true density), and overestimate it elsewhere (as the linear interpolation goes on top of the true density). Since the latter region is larger (in Lesbegue measure, if you like), the trapezoid rule tends to overestimate the integral. Now, as you move to smaller bandwidths, pretty much all of your estimate is piecewise convex, with a lot of narrow spikes corresponding to the data points, and valleys between them. That's where the trapezoid rule breaks down especially badly.

StasK
  • 29,235
  • 2
  • 80
  • 165
  • that means that we are "oversampling" the peaks and "undersampling" the valleys, in some hand-wavy sense. Since the visualization also follows the trapezoidal rule (linear interpolation across samples), it seems too small a kernel bandwidth is also bad for visualization. Also, if we could get a larger number of points at which we calculate the density, there would be less of a problem. – highBandWidth Aug 10 '11 at 01:40
  • 1
    This explanation does not hold water. The problem is that the density is inadequately discretized, not that the trapezoid rule breaks down badly. integrate() is helpless to get a correct answer because density() does not produce a correct representation. To see this, just inspect xy$x: it has only 512 values intended to represent 10,000 narrow spikes! – whuber Aug 10 '11 at 02:02
  • @whuber, that's what the answer said. The point is you need to use the trapezoidal rule for finite number of samples, and it overestimates the area compared to the true density on a continuous axis according to the kernels. My update at the end of the question expands on it. – highBandWidth Aug 10 '11 at 02:07
  • 1
    @high No; the trapezoidal rule is working fine. The problem is that it is working with an incorrect discretization of the integrand. You can't possibly have "a lot of narrow spikes corresponding to the data points" when there are 10,000 data points and only 512 values in the density array! – whuber Aug 10 '11 at 02:10
  • @whuber, of course the trapeziodal rule is working fine for what it is supposed to do (integrating by lin. interp.), but that is a way of understanding why we are consistently getting higher area estimates from the small bw kernels. It is not just a matter of higher variance of the estimate due to lack of precision. The bias for higher estimates is apparently due to the convex nature of the kernels. I'd love to know if convexity has nothing to do with it. – highBandWidth Aug 10 '11 at 14:15
  • @high You're not following me. As far as I can see, this explanation is simply wrong: the gross failure in the integration is not due to errors in the trapezoidal rule. **No** method of integration will work because the sampling frequency of the density is far too coarse. The problem lies in a sampling bias, not in the integration. This is wholly unrelated to convexity. – whuber Aug 10 '11 at 15:02
  • 1
    Looking at these graphs, I am now thinking that the problem is with `density` rather than with `integrate.xy`. With N=10000 and bw=1e-6, you would **have** to see a comb with a height of each tooth of about 1e6, and the teeth being denser around 0. Instead, you still see a recognizable bell-shaped curve. So `density` is cheating on you, or at least it should be used differently with tiny bandwidths: `n` should be about (range of data)/(bw) rather than the default `n=512`. The intergrator must be picking up one of these huge values that `density` returns by an unhappy coincidence. – StasK Aug 10 '11 at 16:10
  • Of course the problem is not with integrate.xy, it is supposed to integrate a set of data, which it does correctly. There are no "errors" in the trapezoidal rule. – highBandWidth Aug 10 '11 at 17:01
  • I think it is not related to convexity since using a kernel that is not convex, such as "triabgular" also has the same bias. It is indeed related to sampling bias. I still contend that it is simply not a lack of precision ("can't do better with 512 pts"), but a systematic bias in the density function to oversample the peaks. Does anyone know where one could find the source code for the density function? – highBandWidth Aug 10 '11 at 17:12
-1

That's okay, you can fix it shifting and scaling; add the smallest number such that the density is non-negative, then multiply the whole thing by a constant such that the area is unity. This is the easy way.

The optimal $L_2$ solution involves "water pouring"; finding the constant $c$ such that $\left[\phi(x)-c\right]^+$ integrates to unity.

Emre
  • 2,564
  • 15
  • 22
  • 2
    Notice that the question is rather on *why* the `density` function does not produce the "proper" density that integrates to 1 - rather then on how to fix it. – Tim Apr 27 '15 at 09:05