3

My question is why Multiple Linear Regression (MLR), based on least squares, cannot be built when the number of variables $(p)$ are larger than the number of samples $(n)$?

Can one explain why is it like this?

TrynnaDoStat
  • 7,414
  • 3
  • 23
  • 39
Learner
  • 789
  • 1
  • 7
  • 16
  • 3
    How many straight lines can you put through a single point? How many planes can you put through two distinct points? What is the problem? Now generalise. – Nick Cox Feb 27 '15 at 12:50
  • 1
    And "MLR" means what? – Wayne Feb 27 '15 at 13:00
  • 1
    @Nick Cox if you have an intercept, you can have only one, if you don't have any dimension you can have as many as you want ! if you have two data points you can have maybe 1 or I don't know. what do you really want to say? – Learner Feb 27 '15 at 13:09
  • I thought you mentioned MLR and LDA multiple times when I first saw your question, but when I edited it just now, to expand MLR to "Multiple Linear Regression", it wasn't there. I don't think I did anything else. At any rate you may want to further edit it to make your MLR v LDA comment part of the question. – Wayne Feb 27 '15 at 13:10
  • 1
    My hope that a hint would clarify for you was unduly optimistic. Others have fleshed out the argument nicely. But note that "if you have an intercept" is precisely what you can not assume in regression. The regression has to find the intercept too. – Nick Cox Feb 27 '15 at 14:43
  • Possible duplicate [here](http://stats.stackexchange.com/questions/118278/regession-diagnostics) – Glen_b Feb 27 '15 at 21:58

4 Answers4

11

I will provide a visual in a very simple case because it is the easiest case to visualize. Imagine you are trying to fit the following linear model: $Y\sim \alpha + X\beta + \epsilon$. In this situation you have two parameters, $\alpha$ and $\beta$, and imagine you only have a sample size of $n=1$.

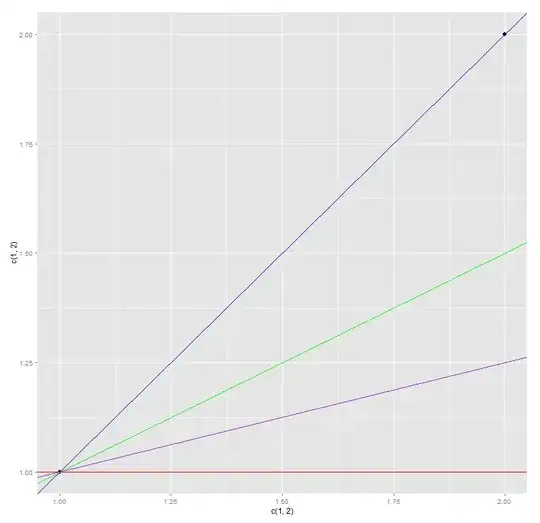
Your single piece of data is represented by the black dot below. Notice all the lines we can fit through this point! Each of these lines are the line of best fit as they all minimize your SSE to 0.

enter image description here

There are in fact infinite lines through this point. You can see this because the data point above is $(1,1)$ and there are infinite solutions to $1=\alpha + \beta$. Now, try to generalize this to thinking of fitting a plane in three dimensional space when you only have two pieces of data $(n=2)$. You will find a similar issue there.

What happens when we try to fit the same model, $Y\sim \alpha + X\beta + \epsilon$, when we have two points of data represented by the two black dots below? In other words, what happens when $n \geq p$?

enter image description here

The blue line above uniquely beats every other line we can draw on this graph in terms of SSE. In other words, there is no other line that would provide as good a fit as the blue line.

If you are not satisfied with a visual explanation, let's think about this in matrix notation. Recall, in multiple linear regression $\hat{\beta}_{p\times1} = [(X^TX)^{-1}X^T]_{p\times n}Y_{n\times1}$. We can equivalently write this as $[(X^TX)^{-1}X^T]_{n\times p}^{-1}\hat{\beta}_{p\times1} = Y_{n\times1}$ by taking the left inverse on each side. If you are familiar with linear algebra, you'll see that $\hat{\beta}$ is the solution to a system of $n$ equations with $p$ unknowns. There is no unique solution to this system when the number of unknowns, $p$, is larger than $n$!

TrynnaDoStat
  • 7,414
  • 3
  • 23
  • 39
  • Thanks for your comment. Unfortunately your explanation is still not simple, e.g. I said we have p (number of variables) >= n (number of samples). Then you explain how many lines goes from a single point ? (it is too vague , please clarify what do you mean with points). As I stated above, there are hundred of such explanation out there, I am looking to find the simplest one for the students (those who do not know anything of statistics ) – Learner Feb 28 '15 at 01:04
  • @Nemo Are you familiar with how the least squares regression line is a "line of best fit" to the data? – TrynnaDoStat Feb 28 '15 at 05:12
  • for sure! I do know how the LS works – Learner Feb 28 '15 at 10:18
  • @Nemo The lines above are LS lines on scatterplots. In the first plot, n=1 and p=2. All of the lines in that plot are LS lines so the line is not unique. In the second plot, n=2 and p=2. Now, there is one unique LS line. – TrynnaDoStat Feb 28 '15 at 14:39
  • Thanks for your time, what you are trying to say, is that when we have one sample and 2 variables, there will be so many LS lines and none is unique while when we have equal n and p, there is at least one unique solution. This is the same as we have 100n and 200p. However, this is just one n and of course we never can find a unique solution, how can we interpret when there are 100n and 200p for example? – Learner Feb 28 '15 at 16:00
  • 2
    @Nemo It's the same idea as the simple 2D example I posted. However, it's impossible to visual the more complicated 200 dimension situation (p=200 means you would have a 200 dimensional scatterplot with n=100 points). Try to generalize the example and visualize a 3D situation (p=3) when we are trying to fit a "plane of best fit" using only n=2 points. Again, there will be no unique plane. – TrynnaDoStat Feb 28 '15 at 16:06
  • I appreciate your time and comments. however, I read some papers saying that you are only able to find unique solution when your p numbers is n-1 (means they should not even be equal and should be 1 variable less than the number of sample) How accurate this is , I don't know ! If you find any 3D visualization, I will be happy to see ! Once again thanks – Learner Feb 28 '15 at 16:11
  • Look my post about pseudo-inverse. It is mathematical solution to the problem of solving system of equations, which LS solution also is. – Analyst Mar 02 '15 at 06:43
6

I believe what Nick was saying in his comment is: your MLR with N variables is trying to fix N values (coefficients) in N-dimensional space, but you are trying to do it with M (M < N) pieces of data. How will you do this?

Since you only have M data points, the other M-N dimensions of your answer are free-floating, as happens when trying to define a line through a single point (2D problem with only one sample) or a plane through two points (3D problem with only 2 samples).

In the case of a line through a point: you have a single sample and you're trying to determine the slope and intercept of a line through it. You can arbitrarily pick a slope and that determines your intercept, or you can arbitrarily pick an intercept and it determines your slope, but you are not doing this from the sample. You have an infinite number of choices, all arbitrary.

If you have two points, the line through them is determined unambiguously. If you have many points and are doing OLS, the line goes through the "center" of the cloud of points in some sense, but it is still unambiguous by the rules of OLS.

Wayne
  • 19,981
  • 4
  • 50
  • 99
  • Thanks for your effort. fine , if you have many points a line goes through the either cloud and then you can still determine slope and intercept for it. so why would it be a problem if we have number of variables = or > than number of samples ? I am searching for a simple explanation to understand why we cannot calculate the regression coefficient ? – Learner Feb 27 '15 at 13:31
  • 2
    @Nemo I think your confusion may stem from the fact that you want an explanation for why we cannot get any values for the coefficients. We can get values, they're just not unique. And what good is a coefficient if there's infinite possibilities for what it could've been? – TrynnaDoStat Feb 27 '15 at 14:30
  • @TrynnaDoStat can we say that for the situation where the P is smaller than n , the coefficients are unique ? I doubt it since we can calculate the standard deviation of regression coefficient which means they varies and not unique!. we all know the basic , theory, concepts and a lot of blah blah (internet is full of info) I am searching for very simple and good explanation of why we cannot build an MLR model when the p >= n ! . so far, I did not see a complete and simple answer – Learner Feb 27 '15 at 15:09
  • 1
    @Nemo When p – TrynnaDoStat Feb 27 '15 at 15:41
3

Analyst's answer is in fact correct. If p>n you end up with an underdetermined system and can use pseudo-inverse to solve it.

When you have more parameters than equations as in this case, using pseudo-inverse finds the minimum euclidian norm solution.

This is the best assumption you can do since this solution has the lowest variance. That is also what you achieve with ridge regression but in a different way. We want this since, given a model $Y=Xb$, if there is noise in measurement $X$ i.e $X_n=X+n$, then estimate $Y=X_n b$ will have an error of $nb$ that its value depends on norm of $b$.

I ignored the constant parameter because one can set it equal to the average of samples and use the above model to estimate the rest.

kon psych
  • 151
  • 4
2

If P, number of variables, is larger than N number of observations then you have underdetermined system of equations.

There exist pseudo-inverse which can solve this:

http://people.csail.mit.edu/bkph/articles/Pseudo_Inverse.pdf

Analyst
  • 2,527
  • 10
  • 11