3

I have started working on a wide (p > n) genetic data set. It is recommended to me to use a regularization technique (such as LASSO or Ridge regression) in order to reduce the number of genes to be used in the logistic regression. Why does logistic regression break down if I use all the genes to predict the outcome ? Is it because of the theory behind it or the implementation of the algorithm for the model ?

DKangeyan
  • 387
  • 1
  • 2
  • 7
  • 1
    It falls down for essentially the same reason [regression does](http://stats.stackexchange.com/questions/118278/regession-diagnostics) when p>n – Glen_b Feb 26 '15 at 10:08
  • Can you explain a bit more, I don't think the question that you referred doesn't go in depth in to explaining it. – DKangeyan Feb 27 '15 at 16:36

1 Answers1

3

Generally speaking you need at least $p$ points to determine $p$ free parameters.

Consider the following simple situation: a logistic regression model, $P[Y=a|x]=\frac{\exp(\alpha+\beta x)}{1+\exp(\alpha+\beta x)}$ or equivalently $\text{logit}(P[Y=1|x])=\alpha+\beta x$, where we only have data at one x-value, say x=5; for which we have two binary outcomes, $y_1=0$ and $y_2=1$; the proportion of $1$'s at $x=5$ is $\frac{1}{2}$.

An infinite number of different logistic functions can be fitted through that point:

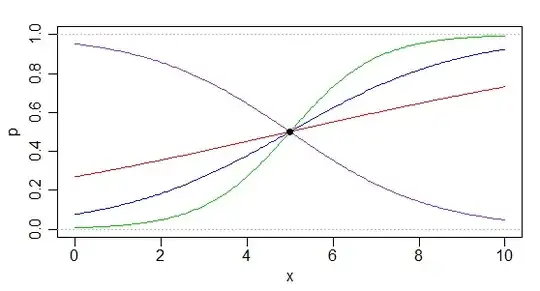
enter image description here

Indeed, any logistic curve which has $\beta = -\alpha/5$ will go through the point. With no data at all, any point in $\mathbf{R}^2$ would be possible. By adding a point $(x_1,y_1)$, a perfect fit can be obtained by any point in the one-dimensional space $\alpha+x_1\beta=\text{logit}(y_1)$ (if we added information at a second value of $x$, the subspace in which $(\alpha, \beta)$ could lie would reduce again, to 0-dimensions (that is - usually - data at two x-values are enough to determine two parameters).

Note that although we're fitting a curve, the equation defining the smaller subspace as we add points is linear in the parameters.

As such, the issues are the same as when $p>n$ in multiple regression.

The answers here and here are therefore relevant.

[If some appropriate form of regularization, constraint or additional criteria are applied, it's generally possible to identify a unique member of the subspace, which is to say the infinite number of solutions can be reduced to a single one.]

Community
  • 1
Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Thank you for the explanation. Would it be correct to say that a logistic model built with p variable for data with n samples where p > n is not identifiable. – DKangeyan Mar 01 '15 at 20:33
  • 1
    Yes, generally there's not enough pieces of information to determine p parameters when p>n -- so nonidentifiable. But it's possible to construct exceptions where p can be smaller but it's still nonidentifiable. We see in my example above, where I had $p\leq n$. With a linear model (a model linear in the *parameters*), the x-values need to span a space of sufficient dimension to determine the parameters (in my example, that wasn't the case). – Glen_b Mar 01 '15 at 22:20