one has also (perhaps implicitly) produced a good estimate of its marginal or conditional distribution.
Point predictions don't necessarily do this.
one must necessarily be able to generate good predictions.
Possibly -- depending on how we define "good"
I'm deliberately leaving the prediction and distribution-fitting methods unspecified.
Okay, then consider prediction using a linear model with a single predictor - one fitted by choosing the slope of the line so as to make the Spearman correlation between residuals and $x$ as close to 0 as possible (if there's an interval at 0, choosing the center of that interval). Rather similar to what was done in this answer to fit a line
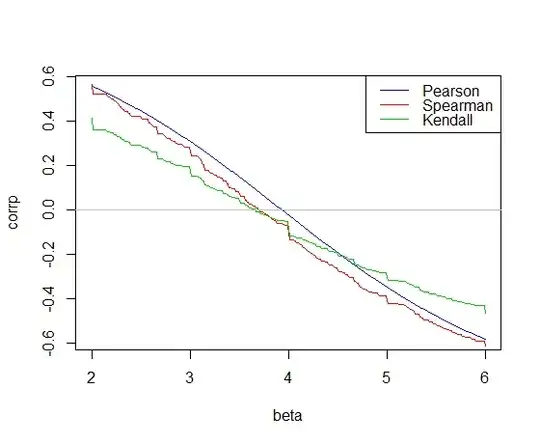
(choosing the slope at which the red 'curve' crosses 0, yielding a slope estimate of $3.714$), except we then proceed with a different intercept obtained from the residuals from the one used in that previous answer. Instead consider this:
Given that slope, estimate the intercept from the $y-\hat{\beta}x$ values using a 3-part Hampel redescending M-estimator of location. (We could do the whole line fit via M-estimation, but I wanted to give some idea of the sheer variety of perfectly reasonable approaches to prediction that are available.)
A point prediction at some $x$, say $x_\text{new}$, is then obtained from the fitted value for that $x$.
So doing that on the cars data in R that I fitted at the other link (using the defaults in robustbase::lmrob with psi="hampel"), I obtained an intercept of $-15.79$.
Resulting in this fitted line:
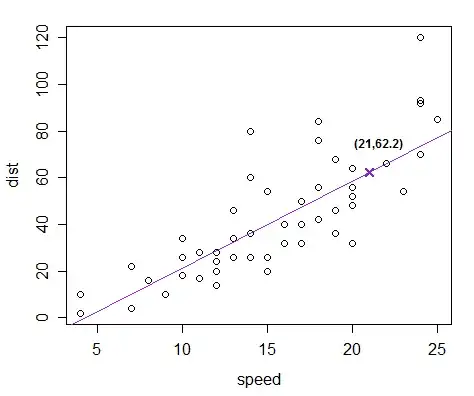
The prediction at $x=21$ is marked in ($62.2$). It appears to be a perfectly reasonable prediction.
We've certainly assumed linearity, but there's no distributional assumption made in obtaining that prediction - the slope was obtained nonparametrically (ie with a distribution free method), while the intercept used M-estimation (and while that grows out of ML estimation, the $\psi$-functions which redescend to 0, such as the Hampel, correspond to no actual distribution).
Clearly point prediction at least needn't involve or relate to a distributional fit, and so the answer to the title question is (demonstrably) "not so".
--
Indeed if we then generated a confidence interval or a prediction interval by bootstrapping, we would have interval prediction without fitting a distribution (unless you call using/re-sampling the ECDF 'fitting', it might well count as estimation depending on what you intend the question to encompass). [However, I think there are also ways to get intervals for some fits generated along similar lines that don't use bootstrapping. For example, we can generate a confidence interval from the slope by inverting the critical values in the Spearman test; at least some kinds of prediction should allow us do something similar for intervals. There are nonparametric tolerance intervals, for example.]

