4

This is a follow-up to to my previous question: How can MANOVA report a significant difference when none of the univariate ANOVAs reaches significance?

I have two IVs with each having three levels and two DVs. MANOVA reported significant main and interaction effects.

I am now facing a new issue which is concerning the possible post-hoc test. What I have done, is to follow up my MANOVA with univariate ANOVAs. However, my univariate analyses (2 of my DVs) did not indicate significance.

I tried reading on Discriminant Function Analysis and want to apply it as another follow-up. However, given that I have two IVs for my [two-way] MANOVA, I would need a Factorial Discriminant Analysis, but am unable to conduct it in SPSS. Does it exist?

Community
  • 1
kea
  • 41
  • 1
  • 4
  • 2
    Here is the original post: http://stats.stackexchange.com/questions/129123. Why do you copy-paste it here? Are you satisfied with the answer there? Can you "accept" it? If you don't have access to your old "kea" account, you can ask StackExchange administrators to merge your accounts. – amoeba Jan 05 '15 at 10:44
  • Hi there @amoeba thank you for your help in the previous post. However, it seems that as it is insignificant, I am unsure of how I will be reporting this in my thesis. Hence I am trying to find out other means of post-hoc rather than running two univariate tests (one for each of my DV). – kea Jan 05 '15 at 10:51
  • 1
    Please edit your post to remove a copy-pasted original post, put a link to the old post to provide the context, and make this one be a separate NEW question. – amoeba Jan 05 '15 at 11:02
  • Here is how you can merge your two accounts: http://meta.stackexchange.com/help/merging-accounts. Please do it. – amoeba Jan 05 '15 at 11:34
  • I further edited your post, please check if everything is according to what you meant. Have you seen this question: [Post-hoc tests for MANOVA: univariate ANOVAs or LDA?](http://stats.stackexchange.com/questions/111044) There might be something useful in the answers. – amoeba Jan 05 '15 at 15:43
  • 1
    Hi in regards to the discriminant analysis, I would just like to ask if it would be fine for me to create an interaction variable to serve as the grouping variable (DV) for the discriminant analysis that correspond to the combination of the 2 IVS used in the MANOVA. Doing so would then just create the new interaction variable with 9 conditions (3x3 of my IVS as mentioned earlier for the MANOVA). Hope that someone can help me with this as I have been unable to find any support in regards to this. – kea Jan 06 '15 at 04:09
  • Ah, I think only now I understand what you meant originally when you said that "seeing that I have two IVs for my MANOVA, I am unable to conduct a Factorial Discriminant analysis on SPSS"*! So the problem is that discriminant analysis is usually run with one factor, and as you have two factors in your MANOVA, you cannot run discriminant analysis with these two factors (SPSS does not allow that). Is that it? Did I understand correctly? Sorry, I did not realize this before. If so, then could you please specify which effects are significant in your MANOVA: one factor? another? interaction? – amoeba Jan 06 '15 at 10:41
  • Hi there @amoeba thanks for the reply. Yes you got that right. My interaction effect was significant in my MANOVA. however the subsequent univariate tests were insignificant. – kea Jan 06 '15 at 18:21
  • @amoeba. I have two IVS and two DVs there was a significant main effect for IV1 on the two combined DVs. However only DV1 was significant at Bonferroni adjustment level of .025. there was a significant main effect for IV2 on the two combined DVs. However none reached significance at Bonferroni adjustment level of .025. Similarly, there was a significant interaction effect between IV1 and IV2 on the combined variables. However analysis of the DVs individually showed no effects for the IVs. Significance for DV1 was .084 while for DV2 it was .146 – kea Jan 07 '15 at 01:54
  • Thank you. I tried to edit your question to make it as clear as possible. I hope I did not edit too much; please double-check that it is still the question you wanted to ask. I hope somebody will answer your question, but if no answer appears I might try it as well. I am not an expert in applied MANOVA though. – amoeba Jan 07 '15 at 02:00
  • @amoeba, thank you very much. Yes it pretty much summarises the question I have in mind. Thank again. – kea Jan 07 '15 at 03:14
  • 1
    kea, I am afraid you forgot to merge your other [unregistered account](http://stats.stackexchange.com/users/63849/kea) with this one. – chl Jan 08 '15 at 14:33

1 Answers1

3

This is a tricky question.

First, here I explained How can MANOVA report a significant difference when none of the univariate ANOVAs reaches significance?

Second, make sure that you understand the difference between using univariate ANOVAs and discriminant analysis as follow-ups for MANOVA; see my answer here: Post-hoc tests for MANOVA: univariate ANOVAs or discriminant analysis? The summary is that you use discriminant analysis if you want to find out which linear combination of your DVs leads to maximum group separability (usually in order to try to interpret this linear combination). This linear combination is called "[first] discriminant axis".

Third, as you say, there is no such thing as "factorial LDA"; I don't know about SPSS specifically, but I've never seen "factorial LDA" mentioned in the literature (I use "LDA" to refer to linear discriminant analysis). However, MANOVA is very intimately related to LDA, as I explain here in much detail: How is MANOVA related to LDA? So if you understand the math behind MANOVA/LDA, you can manually obtain discriminant axis for each of your factors -- i.e. three discriminant axes in total (for factor A, factor B, and for interaction AB). See in particular the Update to my answer in the linked post, regarding factorial MANOVA. I cross-post here my figure from that thread as an appetizer:

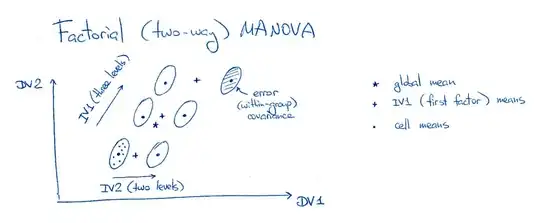
factorial MANOVA and LDA

Note that these will be three different axes, i.e. three different linear combinations. What you suggested in the comments (to create a new "composite" interaction variable with 9 conditions and use it for LDA) is smart and not entirely meaningless, but would only result in one single [most discriminative] axis, and that is not what you probably want here. Instead, you want to see which linear combination of your DVs best separates levels of factor A, which one -- levels of factor B, which one -- levels of AB.

I have no idea whether this is implemented in SPSS (or in any other package); in the worst case, you might need to go through the computations yourself.

Community
  • 1
amoeba
  • 93,463
  • 28
  • 275
  • 317
  • I believe that "factorial DA" is used in place of Canonical Discriminant Analysis, and in this case this is usually applied for descriptive, not predictive, purpose. – chl Jan 08 '15 at 14:40
  • @chl: Thanks, I am glad to see you here. I am not an expert on MANOVA and only know about it because I am working with dimensionality reduction and am well familiar with PCA/LDA/CCA etc. But mostly I find that questions on MANOVA attract almost no interest at all on CV and often seem to remain unanswered unless I try to answer them... I have just edited my answer to restructure it a bit and provide a figure. ... – amoeba Jan 08 '15 at 14:46
  • ... Re your comment: what *is* Canonical Discriminant Analysis? If you mean [this](http://en.wikipedia.org/wiki/Linear_discriminant_analysis#Canonical_discriminant_analysis_for_k_classes), then I prefer to call it simply LDA (it would be weird to restrict the name "LDA" to only two groups). And yes, here I am only talking about dimensionality reduction part of LDA, not the classification part. In any case, Wikipedia says it's LDA with more than 2 groups (levels of one factor), whereas here we need more than 1 factor... – amoeba Jan 08 '15 at 14:47
  • Hi there @amoeba, so sorry but i am unable to understand the explanation that you provided over at -How can MANOVA report a significant difference when none of the univariate ANOVAs reaches significance?- The purpose of asking this question is that I am currently conducting my hypotheses testing and that since the multivariate is significant and that the univariate is insignificant, do I just report that there was a significant multivariate effect but after concluding that the univariate effect is not significant. I should leave it as that – kea Jan 09 '15 at 11:36
  • @kea: Hmmm... Sorry that my explanation in your previous question was not clear enough. Do you maybe want to ask some clarifying questions? I guess it's better to do it in the comments to *that* answer though. Regarding your reporting: well, of course you can report that multivariate effect was significant but univariate not! Whether you can leave it like that or need to explore further, I cannot tell you, this depends on your research question, purpose of this analysis, etc. etc. – amoeba Jan 09 '15 at 11:41
  • hi @amoeba do you think I can explore it as the significant value for one of them is at.08? – kea Jan 09 '15 at 11:53
  • I think you misunderstand, @kea. 0.08 is not a significant p-value, there is nothing to explore here. What you have is that both DVs do not separate your groups well. But together they do. This means that there is some linear combination of them that does separate groups. The purpose of discriminant analysis is to find out what linear combination that is. I cannot tell you if you should care about it or not, that's for you to decide. – amoeba Jan 09 '15 at 11:58
  • Hi there @amoeba. Thanks for your reply as always. Will it then be possible to justify an analysis theory wise. In that one of this DV has been shown to be more important than the other in past studies in separating the groups. – kea Jan 09 '15 at 13:35
  • Sorry, @kea, I don't get the question. Will it be possible to justify what analysis? You can perform any analysis on Earth; the question of what would be *interesting* and *relevant* for your research, only you can answer. – amoeba Jan 09 '15 at 14:03
  • 1
    In R, function candiscList() from "candisc" package "performs a generalized canonical discriminant analysis for all terms in a multivariate linear model" (ref: candiscList help page). See also a worked example of two-way canonical discriminant analysis in section 4.2 of the first reference in the help page of the heplot() function from "heplots" package. Hope this helps ! – Rodolphe Jul 31 '15 at 16:14
  • 1
    @Rodolphe: Wow, thanks for this pointer. I guess you refer to the papers by Michael Friendly, such as [HE Plots for Multivariate Linear Models](http://euclid.psych.yorku.ca/datavis/papers/jcgs-heplots.pdf) (2007) and [Data Ellipses, HE Plots and Reduced-Rank Displays for Multivariate Linear Models: SAS Software and Examples](http://www.jstatsoft.org/v17/i06/paper) (2006). Very interesting! – amoeba Jul 31 '15 at 16:37