6

I would just like to ask if it is normal for the values from my multivariate tests to be significant but for the values from my univariate tests of between-subjects effects table to be insignificant.

I have conducted a 3x3 between group MANOVA and it seems that there is a multivariate effect where there appeared to be a statistically significant difference between my independent variables on the combined dependent variables.

However, when the results for the dependent variables were considered separately, none of them reached statistical significance.

I am pretty much stumped by this as I believe that it should be significant for at least one of my dependent variables but it does not appear to be the case.

amoeba
  • 93,463
  • 28
  • 275
  • 317
kea
  • 63
  • 1
  • 3
  • 1
    It's quite easy for the groups to be indistinguishable on any of the margins (the univariate tests), yet the multivariate distribution can be clearly different. [This answer](http://stats.stackexchange.com/a/61129/805) shows an example that illustrates this issue. With more variates, the effect can be more pronounced. – Glen_b Dec 15 '14 at 11:14
  • @Glen_b: The same figure as in your linked answer posted here together with p-values for MANOVA and both ANOVAs would constitute a great answer... – amoeba Dec 15 '14 at 12:00
  • 1
    @Glen_b: I ended up making a similar simulation myself. – amoeba Dec 22 '14 at 13:02
  • @amoeba yes, thanks -- I was much too slow about getting back to this one. – Glen_b Dec 22 '14 at 14:36

1 Answers1

9

Here is a figure illustrating how it is possible:

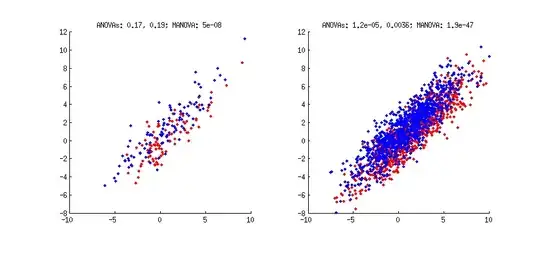
enter image description here

Two populations (red and blue) are sampled from a same 2D distribution, but slightly shifted from each other. On the left $N=100$, on the right $N=1000$ in each group. In both cases, I conduct two univariate ANOVAs (for $x$ dimension and for $y$ dimension) and one multivariate MANOVA.

P-values are reported in the titles. Note that on the left, both univariate tests yield non-significant p-values of around $0.2$, whereas MANOVA reports a very significant one. This happens because to separate the groups the data need to be projected onto a diagonal running from upper-left to lower-right corner of the subplot; projecting the data on either horizontal or vertical axes would not result in significant separation of the two groups. Finding such "optimal group-separating projection" is what discriminant analysis (LDA) and MANOVA both do (directly or indirectly).

It might not be obvious from the left figure that there is any difference between groups at all, but it should be evident on the right figure, where more points are sampled from the same distributions. Here univariate tests reach significance as well, but MANOVA is of course still much more sensitive.

[Note that in case of only one factor with only two levels (i.e. only two groups) ANOVA is equivalent to a t-test, and MANOVA is equivalent to a Hotelling's T2-test.]

Simulation code (Matlab):

Ns = [100 1000];

figure
for i=1:2
    subplot(1,2,i)

    X = randn(Ns(i),2);
    X = bsxfun(@times, X, [4 1]);
    X = X * [sind(45) cosd(45); cosd(45) -sind(45)];
    X = bsxfun(@plus, X, [1.5 1]);

    Y = randn(Ns(i),2);
    Y = bsxfun(@times, Y, [4 1]);
    Y = Y * [sind(45) cosd(45); cosd(45) -sind(45)];
    Y = bsxfun(@plus, Y, [1 1.5]);

    hold on
    scatter(X(:,1), X(:,2), 'r.')
    scatter(Y(:,1), Y(:,2), 'b.')
    axis([-10 10 -8 12])
    axis square

    [~, p1] = ttest2(X(:,1), Y(:,1));
    [~, p2] = ttest2(X(:,2), Y(:,2));
    [~, p3] = manova1([X; Y], [ones(size(X),1); 2*ones(size(X),1)]');

    title(['ANOVAs: ' num2str(p1,2) ', ' num2str(p2,2) '; MANOVA: ' num2str(p3,2)])
end
amoeba
  • 93,463
  • 28
  • 275
  • 317