7

I have measured a continuous outcome variable in three groups of patients, where the groups are related to the severity of disease (control, mild disease, severe disease). I would like to test for a "trend" among these three groups--that is, does the continuous variable become "worse" from control to mild to severe.

  1. Is it possible/sensical to test for trend in this type of data?
  2. If so, what tests should I consider/research?
  3. Could you recommend an R package that would carry out this analysis?

Best, and thanks,

--Davis

sudo make install
  • 242
  • 1
  • 3
  • 9

4 Answers4

3

Very late answer but you might find this question, and this post helpful. Personally, I would just run a linear model with the categories represented as (ordered) integers, and examine the coefficient.

There is also some nice guidance in the BMJ stats series.

Community
  • 1
drstevok
  • 530
  • 5
  • 18
1

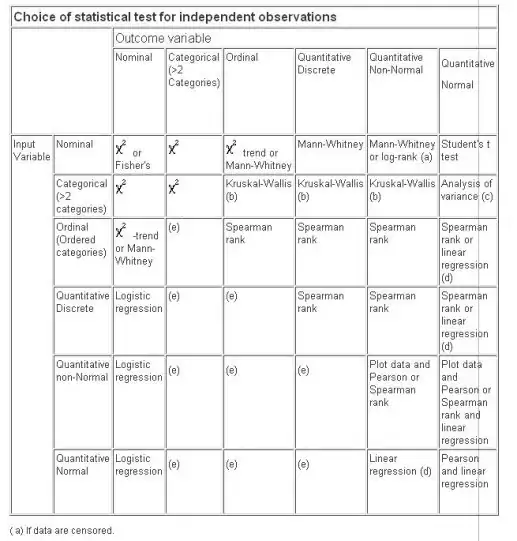
The first step is to plot the three histograms and see how much they overlap. If there is enough data to make a histogram (40+ samples) that can be used to identify if the distribution in each category is normally distributed or not, and they are normally distributed then doing t-test for paired means and Levene's test for difference in variance (i.e., standard deviation squared) will be powerful and allow for determining whether or not there is an organized difference between the groups either with respect to location of the continuous variable or its variability. Doing these tests as one-sided tests would allow for identifying how they rank with respect to each other, e.g. A>B>C or not. If there are fewer than 40 samples in each group, or if there is no method by which one can normalize the data, for example by taking reciprocals, logarithms, etc., then one should use Wilcoxon for difference of location and Conover for difference of variance as those "non-parametric" tests rank the results and do not require normal conditions for their use.

Carl
  • 11,532
  • 7
  • 45
  • 102
0

Jonckheere-Terpstra test is the tool you was probably looking for.

Karolis Koncevičius
  • 4,282
  • 7
  • 30
  • 47
carlo
  • 4,243
  • 1
  • 11
  • 26
0

The R package brms (Bayesian regression models using Stan) can use Bayesian estimation to fit models with ordinal predictors. brms can handle a wide range of designs (e.g. multivariate and/or longitudinal and/or hierarchical) and a wide range of distributions (counts, ordinal outcomes, continuous outcomes, censored, etc. etc.). It can also incorporate temporal and spatial auto-correlation and fit mixture models. The author of brms, Paul Buerkner, has provided a large number of vignettes to demonstrate how to use the package's many features. You can see the one for monotonic ordinal predictors at: https://cran.r-project.org/web/packages/brms/vignettes/brms_monotonic.html

Jonathan Williams
  • 1