Why not log-transform all variables that are not of main interest?

Question

Books and discussions often state that when facing problems (of which there are a few) with a predictor, log-transformimg it is a possibility. Now, I understand that this depends on distributions and normality in predictors is not an assumption of regression; but log transforming does make data more uniform, less affected by outliers and so on.

I thought about log transforming all my continuous variables which are not of main interesr, ie variables I only adjust for.

Is that wrong? Good? Useless?

Answer 1

Now, I understand that this depends on distributions and normality in predictors

log transforming does make data more uniform

As a general claim, this is false --- but even if it were the case, why would uniformity be important?

Consider, for example,

i) a binary predictor taking only the values 1 and 2. Taking logs would leave it as a binary predictor taking only the values 0 and log 2. It doesn't really affect anything except the intercept and scaling of terms involving this predictor. Even the p-value of the predictor would be unchanged, as would the fitted values.

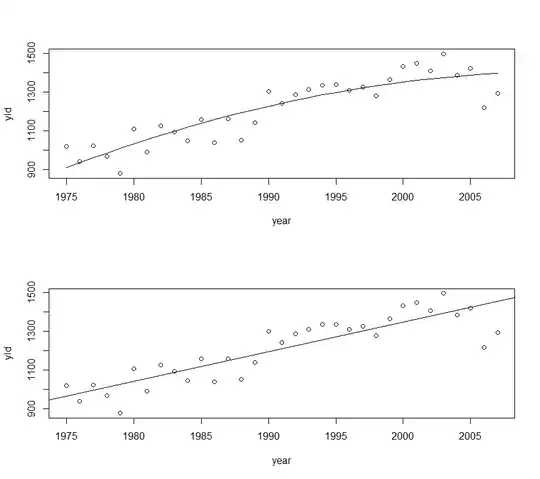
ii) consider a left-skew predictor. Now take logs. It typically becomes more left skew.

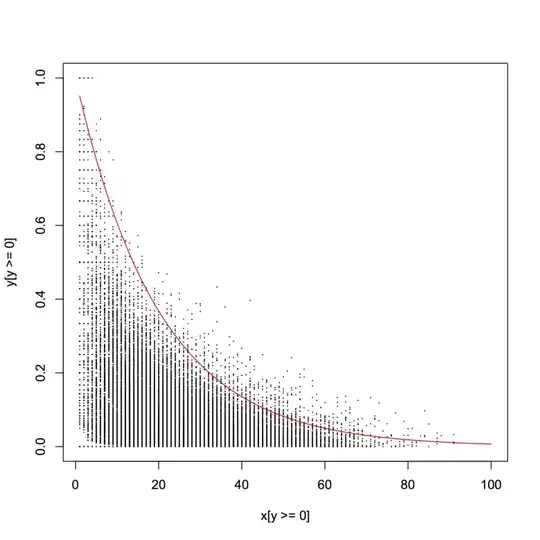
iii) uniform data becomes left skew

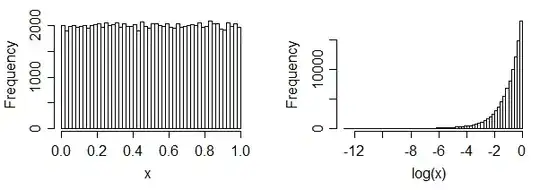
(it's often not always so extreme a change, though)

less affected by outliers

As a general claim, this is false. Consider low outliers in a predictor.

I thought about log transforming all my continuous variables which are not of main interest

To what end? If originally the relationships were linear, they would not longer be.

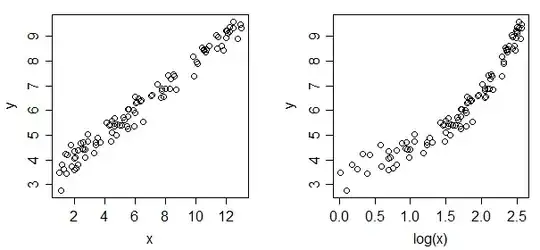
And if they were already curved, doing this automatically might make them worse (more curved), not better.

--

Taking logs of a predictor (whether of primary interest or not) might sometimes be suitable, but it's not always so.

Answer 2

In my opinion, it doesn't make sense to perform log transformation (and any data transformation, for that matter) just for the sake of it. As previous answers mentioned, depending on data, some transformations would be either invalid, or useless. I highly recommend you to read the following IMHO excellent introductory material on data transformation: http://fmwww.bc.edu/repec/bocode/t/transint.html. Please note that code examples in this document are written in Stata language, but otherwise the document is generic enough and, thus, useful to non-Stata users as well.

Some simple techniques and tools for dealing with common data-related problems, such as lack of normality, outliers and mixture distributions can be found in this article (note, that stratification as an approach to dealing with mixture distribution is most likely the simplest one - a more general and complex approach to this is mixture analysis, also known as finite mixture models, a description of which is beyond the scope of this answer). Box-Cox transformation, briefly mentioned in the two references above, is a rather important data transformation, especially for non-normal data (with some caveats). For more details on Box-Cox transformation, please see this introductory article.

Answer 3

Log transforming does not ALWAYS make things better. Obviously, you can't log-transform variables that achieve zero or negative values, and even positive ones that hug zero could come out with negative outliers if log-transformed.

You should not just routinely log everything, but it is a good practice to THINK about transforming selected positive predictors (suitably, often a log but maybe something else) before fitting a model. The same goes for the response variable. Subject-matter knowledge is important too. Some theory from physics or sociology or whatever might naturally lead to certain transformations. Generally, if you see variables that are positively skewed, that's where a log (or maybe a square root or a reciprocal) might help.

Some regression texts seem to suggest that you have to look at diagnostic plots before considering any transformations, but I disagree. I think it's better to do the best job you can at making these choices before fitting any models, so that you have the best starting point possible; then look at diagnostics to see if you need to adjust from there.