So I'm trying to determine whether the residuals from a seasonal ARIMA model are normal or not. Upon using the shapiro wilk test, I get a staggeringly low p-value leading me to think that the residuals are in fact non-normal. However, my qqplot seems acceptable for a decently large number of observations(~700). Shapiro-Wilk normality test
data: residuals(housing.arima)
W = 0.979, p-value = 3.345e-08
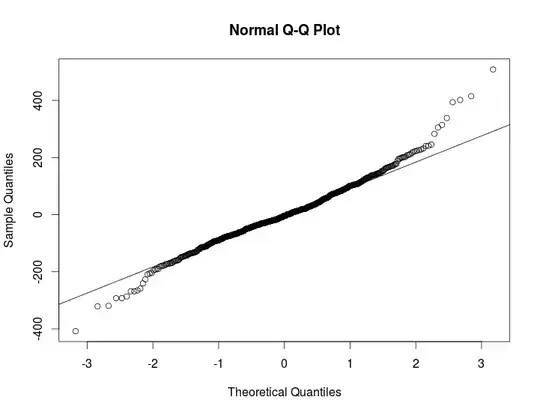
In terms of exploratory data analysis, what's the standard thing for someone to do from here onwards, should I operate under the assumption that the residuals are not normal or otherwise? And also, are there any normality tests that are not as sensitive to the sample size?