3

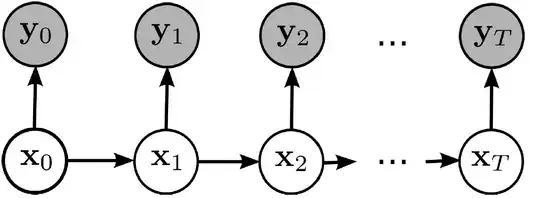
My goal is to find closed form equations for posterior marginals $P(x_n|y_0, ... , y_n)$ in a general HMM.

I was told that we can calculate it exactly via BP (belief propagation, thought not sure how BP comes in the picture...) in an iterative manner in two steps:

Prediction step: Transitioning to a new state:

$$p(x_{n+1} | y_0, ..., y_n) = \int_{x_n}p(x_{n+1}|x_{n}) p(x_{n}|y_0, ... , y_n) dx_n $$

Update: Folding in a new observation:

$$p(x_{n+1} | y_0, ..., y_{n+1}) = \frac{1}{Z}p(y_{n+1} | x_{n+1}) p(x_{n+1}|y_0, ... , y_n)$$

I was also told that Z is the partition function which is an implicit integral.

However, I did not understand the mathematical correctness of the update equation. Does someone know why that is mathematically correct?

I guess what confuses me is that its not clear to me how to use probabilities calculated in the prediction step can be used to calculate the next hidden state in an HMM and include the new observation.

Also, how is this using belief propagation? Is the integral somewhere suppose to be a message as in BP?

This is what I have tried:

$$p(x_{n+1} | y_0, ..., y_{n+1}) = \frac{p(x_{n+1}, y_0, ... y_n, y_{n+1}) }{p(y_0, ..., y_n, y_{n+1} )} = \frac{p(y_{n+1}| x_{n+1}, y_0, ... y_n,)p(x_{n+1}, y_0, ..., y_n)}{p(y_0, ..., y_n, y_{n+1} )}$$

By the conditional independencies implies by the graphical model of an HMM we have $p(y_{n+1}| x_{n+1}, y_0, ... y_n,) = p(y_{n+1}| x_{n+1})$

$$ \frac{p(y_{n+1}| x_{n+1})p(x_{n+1}, y_0, ..., y_n)}{p(y_0, ..., y_n, y_{n+1} )}$$

Doing hayes rule again we get:

$$ \frac{p(y_{n+1}| x_{n+1})p(x_{n+1} | y_0, ..., y_n) p(y_0, ... , y_n)}{p(y_0, ..., y_n, y_{n+1} )}$$

Which if my math is correct means that the partition function is:

$$ \frac{1}{Z} = \frac{ p(y_0, ... , y_n) }{p(y_0, ... , y_n, y_{n+1}} )$$

Which doesn't involve any implicit integral as far as I can tell... am I doing something wrong? Does this seem correct?

I do know that the partition function is suppose to normalize a normalized probability distribution, however, I don't see why it matters in this context... is that what it refers to as an implicit integral?

Charlie Parker
  • 5,836
  • 11
  • 57
  • 113

1 Answers1

1

The dependency structure of a HMM is described by this graph.

HMM

Absence of an arrow connecting two random variables means that they are conditionally independent given the values of their parents.

Using the law of total probability and the product rule you have $$ p(x_{n+1}\mid y_0,\dots,y_n) = \int p(x_{n+1},x_n\mid y_0,\dots,y_n)\,dx_n $$ $$ = \int p(x_{n+1}\mid x_n,y_0,\dots,y_n)\,p(x_n\mid y_0,\dots,y_n)\,dx_n \, . $$

Inspecting the graph you will find that if you are given the value of $x_n$, then $x_{n+1}$ and $y_0,\dots,y_n$ are conditionally independent. Hence, $p(x_{n+1}\mid x_n,y_0,\dots,y_n)=p(x_{n+1}\mid x_n)$ and you have the first desired equation.

From the definition of conditional probability / density and the product rule, you have $$ p(x_{n+1}\mid y_0,\dots,y_{n+1}) \propto p(x_{n+1},y_0,\dots,y_{n+1}) $$ $$ \propto p(y_{n+1}\mid x_{n+1},y_0,\dots,y_n)\,p(x_{n+1}\mid y_0,\dots,y_n) \, , $$ in which $\propto$ means proportionality up to terms that do not depend on $x_{n+1}$. Inspecting the graph you will find that if you are given the value of $x_{n+1}$, then $y_{n+1}$ and $y_0,\dots,y_n$ are conditionally independent. Hence, $p(y_{n+1}\mid x_{n+1},y_0,\dots,y_n)=p(y_{n+1}\mid x_{n+1})$ and you get the desired result.

The normalization constant is $$ Z=\int p(y_{n+1}\mid x_{n+1}) \, p(x_{n+1}\mid y_0,\dots,y_n)\,dx_{n+1} \, . $$

If you find the $\propto$ reasoning above confusing, write things out explicitly (and tediously). $$ p(x_{n+1}\mid y_0,\dots,y_{n+1}) = \frac{p(x_{n+1},y_0,\dots,y_{n+1})}{p(y_0,\dots,y_{n+1})} $$ $$ = \frac{p(y_{n+1}\mid x_{n+1},y_0,\dots,y_n)\,p(x_{n+1}\mid y_0,\dots,y_n)\,p(y_0,\dots,y_n)}{p(y_0,\dots,y_{n+1})} $$

Therefore, $$ Z = \frac{p(y_0,\dots,y_{n+1})}{p(y_0,\dots,y_n)} \, . $$ But, especially if you are planning to do some Bayesian inference, get confortable with $\propto$ computations. For instance, check this one.

Community
  • 1
Zen
  • 21,786
  • 3
  • 72
  • 114
  • so the partition function Z is different for each "update" step that we do? i.e. $Z = p(y_0, ..., y_{n+1} ) = \int_{x_{n+1}} p(y_{n+1} | x_{n+1}) p(x_{n+1} | y_0,...y_n ) dx_{n+1}$ ? i.e. its different because we include a new observation at each step? – Charlie Parker Dec 07 '14 at 02:35
  • I might be wrong, but I can't see why what you wrote is correct. Notice you first step implies that: $$p(x_{n+1}, y_0, ... , y_{n+1}) = p(y_{n+1}|x_{n+1},y_0,...y_n)p(x_{n+1}|y_0, ... y_n) = \frac{p(y_{n+1}, x_{n+1},y_0,...y_n)}{p(x_{n+1}, y_0,...y_n)} \frac{p(x_{n+1}, y_0, ... y_n)}{p(y_0, ... y_n)} = \frac{p(y_{n+1}, x_{n+1},y_0,...y_n)}{p(y_0, ... y_n)}$$. Which implies the partition function is what I wrote in my original question/post. i.e. your missing a $p(y_0,...y_n)$ or...I have an extra term that should go away for some reason... – Charlie Parker Dec 07 '14 at 02:54
  • which I believe your missing a factor of $1 / p(y_0, ..., y_{n+1})$ and thus your equality on the numerator for the joint doesn't hold...or did I make a mistake? – Charlie Parker Dec 07 '14 at 02:59
  • what do you think? – Charlie Parker Dec 07 '14 at 15:21
  • 1
    Forget about terms that do not depend on $x_{n+1}$ and normalize at the end. – Zen Dec 07 '14 at 15:25
  • And don't lie, Pinocchio. – Zen Dec 07 '14 at 15:26
  • 1
    Thanks Zen! Your answer makes sense. Though its a little strange (at least for me) that the partition function is defined over the conditional (instead of the joint of the original model). I guess I am just more used to calling the partition function to the constant that normalizes the original model involving all the x's and y's. Regardless, if its "correct" to call this specific Z partition or not, your answer is definitively mathematically sound! – Charlie Parker Dec 07 '14 at 15:46
  • 1
    Btw, I will use all my statistics and knowledge of HMM's to lie as much as I want! muahahaha :p – Charlie Parker Dec 07 '14 at 15:47
  • 1
    Thanks for the extra explanation! Both of your answers make sense to me, thanks so much! :) Unfortunately, I can't accept your answer nor up vote you more :p – Charlie Parker Dec 07 '14 at 15:48
  • 1
    OK, but that may give you a longer nose. By the way, it's interesting to notice that the normalization constant can be computed either by doing an integral or just by finding the ratio of two densities. This is similar to the "candidate's formula" of Julian Besag. – Zen Dec 07 '14 at 15:58