The formula for SE of risk ratios: $\sqrt{1/a - 1/(a+c) + 1/b - 1/(b+d)}$ Where a+c is group1 and b+d is group2. Then for the confidence interval we add/subtract the result to/from natural log of the ratio.
While ratio is expressed in log, why isn't SE expressed in log? How did people come with the above mentioned formula? I couldn't find any prof on the Internet, don't want to take it for granted :)
Here is the derivation. I use the same notation as in this presentation (starting from page 29). Let's look at the familiar $2\times2$-Table below.
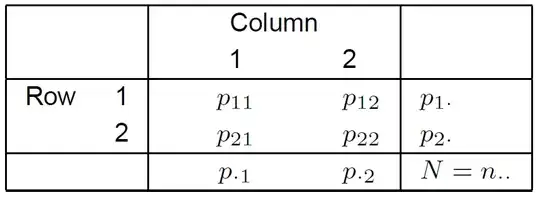
The relative risk or risk ratio is defined as $$ \theta=\mathrm{RR}=\dfrac{\dfrac{p_{11}}{p_{11}+p_{12}}}{\dfrac{p_{21}}{p_{21}+p_{22}}}=\dfrac{p_{11}\cdot (p_{21}+p_{22})}{p_{21}\cdot (p_{11}+p_{12})} $$ We want to derive the variance of $\theta$. The multivariable version of the delta method is: $$ \mathrm{Var}(\hat{\theta})\approx \nabla f(p_{11}, p_{12}, p_{21}, p_{22})\cdot \mathrm{Cov}(p_{11}, p_{12}, p_{21}, p_{22})\cdot \nabla f(p_{11}, p_{12}, p_{21}, p_{22})^{T} $$ Where $\nabla$ is the gradient vector. That is: $$ \nabla f(p_{11}, p_{12}, p_{21}, p_{22}) = \left(\frac{\partial f}{\partial\,p_{11}}, \ldots,\frac{\partial f}{\partial\,p_{22}}\right) $$ We want to estimate $$ \mathrm{Var}(\log(\mathrm{RR}))=\mathrm{Var}\left[\log\left(\frac{p_{11}\cdot (p_{21}+p_{22})}{p_{21}\cdot (p_{11}+p_{12})}\right)\right] $$ Let the function $f$ be $$ f = \left[\log(p_{11}) + \log(p_{21}+p_{22}) - \log(p_{21}) - \log(p_{11}+p_{12})\right] $$ The gradient $\nabla f$ is $$ \nabla f = \left(\frac{p_{12}}{p_{11}^{2}+p_{11}p_{12}},-\frac{1}{p_{11}+p_{12}},-\frac{p_{22}}{p_{21}^{2}+p_{21}p_{22}}, \frac{1}{p_{21}+p_{22}}\right) $$ The variance covariance matrix for a multinomial distribution with $c=4$ categories is $$ \Sigma=\frac{1}{n}\left( \begin{array}{cccc} \left(1-p_{11}\right) p_{11} & -p_{11} p_{12} & -p_{11} p_{21} & -p_{11} p_{22} \\ -p_{11} p_{12} & \left(1-p_{12}\right) p_{12} & -p_{12} p_{21} & -p_{12} p_{22} \\ -p_{11} p_{21} & -p_{12} p_{21} & \left(1-p_{21}\right) p_{21} & -p_{21} p_{22} \\ -p_{11} p_{22} & -p_{12} p_{22} & -p_{21} p_{22} & \left(1-p_{22}\right) p_{22} \\ \end{array} \right) $$ Then $\nabla f\,\Sigma$ equals $$ \nabla f\,\Sigma=\frac{1}{n}\times \left[\frac{p_{12}}{p_{11}+p_{12}}, -\frac{p_{12}}{p_{11}+p_{12}}, -\frac{p_{22}}{p_{21}+p_{22}}, \frac{p_{22}}{p_{21}+p_{22}}\right] $$ Now we need $(\nabla f\,\Sigma)\times \nabla f^{T}$ which equals: $$ (\nabla f\,\Sigma)\times \nabla f^{T}=\frac{1}{n}\times \left[-\frac{1}{p_{11}+p_{12}}+\frac{1}{p_{21}}-\frac{1}{p_{21}+p_{22}}+\frac{1}{p_{11}}\right] $$ Substituting the MLEs for $\widehat{p_{ij}}=n_{ij}/n$ finally yields $$ \widehat{\mathrm{Var}(\log(\mathrm{RR})}=\left(\frac{1}{n_{11}}+\frac{1}{n_{21}}\right)-\left(\frac{1}{n_{11}+n_{12}}+\frac{1}{n_{21}+n_{22}}\right) $$ So the approximative standard error for the relative risk on the log-scale is $$ \widehat{\mathrm{SE}(\log(\mathrm{RR})}=\sqrt{\widehat{\mathrm{Var}(\log(\mathrm{RR})}}=\sqrt{\left(\frac{1}{n_{11}}+\frac{1}{n_{21}}\right)-\left(\frac{1}{n_{11}+n_{12}}+\frac{1}{n_{21}+n_{22}}\right)} $$ So an approximative two-sided confidence interval of level $\alpha$ for the relative risk on the original scale is $$ \mathrm{CI}=\exp(\log(\mathrm{RR})\pm z_{1-\alpha/2}\times \mathrm{SE}(\log(\mathrm{RR})) $$
