3

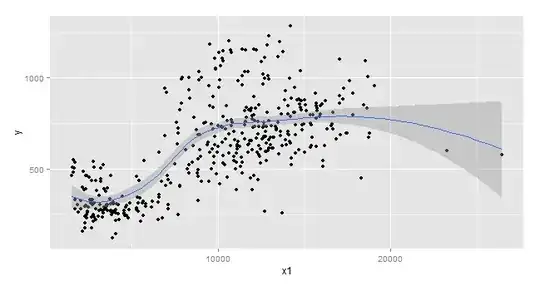
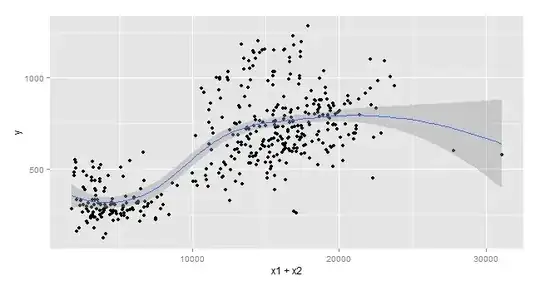
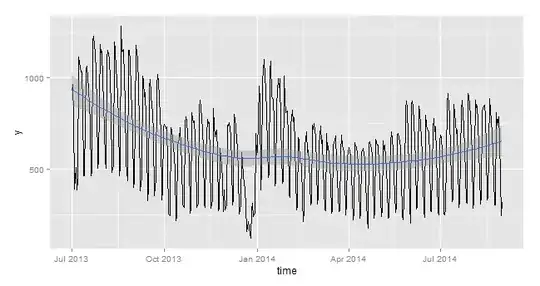
I have two continuous predictors ($x_1, x_2$) in my data set and a continuous response variable $y$. The data set is by date for 6 quarters. Since I observed a clear pattern of surge during weekday vs. weekend, I created a dummy variable ($x_3$) like an on.off switch with 0.50 if it is Saturday / Sunday and 1 otherwise. The $x_1$ and $x_2$ in my data have two easily separable levels - meaning low on weekends and regular on weekdays.

The model specification i was trying out is: $log(y) = \alpha + \beta x_1x_3 + \beta x_2x_3 + \epsilon $

First Question: Is the dummy variable a good idea? or Should I make separate models. My objective is to predict $y$ as accurately as possible.

Second Question: When I checked my MAPE and preidcted values based on above fit, I realized the following: I am under-predicting always for Quarter 3 and over predicting for Q4 and Q1. This points to some kind of seasonality. How can I accomodate this in the model?

Third Question: Public Holidays are other days when the model is over-predicting $y-hat$ by huge % but $y$ slumps precipitously. Is it a good idea to remove these days from my model set?

Given below are scatter plots and y plotted against time of my data set: enter image description here enter image description here enter image description here enter image description here

vagabond
  • 375
  • 1
  • 2
  • 14
  • If this is time series data why aren't you trying to model it as such, e.g. AR(p). You'll be able to use your $x_1, x_2$ as well. – James Nov 21 '14 at 19:06
  • Not sure I'm following what you are saying . . . – vagabond Nov 21 '14 at 19:10
  • I found this link to be extremely helpful - http://stats.stackexchange.com/questions/21282/regression-based-for-example-on-days-of-week?rq=1 and http://www.ats.ucla.edu/stat/r/library/contrast_coding.htm – vagabond Nov 21 '14 at 19:27

1 Answers1

4

Adding dummy variables is a great methodology for accounting for causal impact/attribution of y to specific events. To account for quarters and holidays, you should add more dummy variables to your data. While you should be wary of adding too many dummy variables and causing over-generalization (aka "overfit"), it sounds like your sample is large enough to make it ok to add a few more... for example, I would probably not make a separate dummy var for each holiday, but rather just a single holiday dummy variable (assuming all holidays have a similar effects on y). To add dummy variables, one can create contrast matrix for categorical variables. Explained with example here: http://www.ats.ucla.edu/stat/r/library/contrast_coding.htm

Caution: More and more dummy variables, make the model output more and more difficult to interpret and explain though you may score high on prediction on your model training set.

A related question on CV has a great answer: Regression based for example on days of week

The most obvious next step is to add time to the model. This is easy if your measurements occur at equal time intervals: you just need to convert from time to # of intervals since the first measurement (so the first measurement = 0). Adding this variable will take care of the "trend" portion of a time series, much like the dummy variables are taking care of the seasonality/causal events in the model.

If you want to dig into more complicated models (like autoregression, ARIMA, etc.), I cannot recommend this (open and free) book enough: Forecasting: principles and practice by Rob J Hyndman and George Athana­sopou­los, I suspect that you would find it extremely useful- it has all the basics you need to know for forecasting, and some great R code to go along with it. The authors are very well respected in the field.

Community
  • 1
TLJ
  • 828
  • 1
  • 6
  • 13