This is a simple question but I am new regression analysis.
If my regression model is of the specification,
$\ln(y) = \alpha + \beta_1 X_1^2 + \beta_2 X_2^2 + \epsilon $,
and I have estimated the $\beta_1, \beta_2, \alpha$ values, how can I predict the $y$ values on the original scale?
Here are the scatter plots:
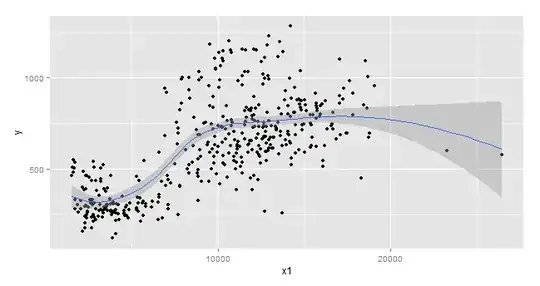

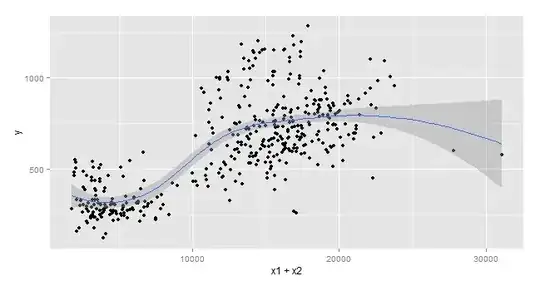
Here is $y$ plotted against time:
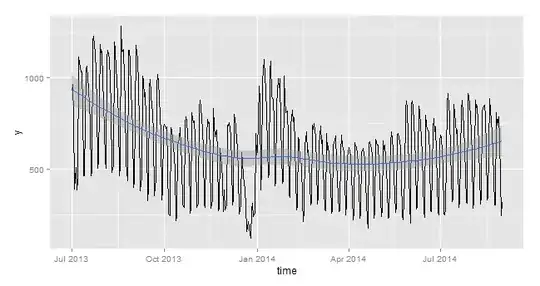
thanks.