I am estimating a (semi)parametric and a parametric model for a panel data set, and I want to test the functional form by applying the method proposed by Henderson et al. (2008, p.266–267). In particular, given the two models:
$$ \begin{aligned} Y &= X^T\beta + Z^T\gamma + u\quad(\textrm{parametric})\\ Y &= X^T\beta + \theta(Z) + u\quad(\textrm{semi-parametric}) \end{aligned} $$
They use $H_0$ to denote the null hypothesis of the linear regression model, against $H_1$, the corresponding alternative is the semiparametric model. Letting $\tilde{\beta}, \tilde{\gamma}$ represent consistent estimates of the parameters from the parametric model and $\hat{\beta}, \hat{\gamma}$ represent consistent estimates of the parameters from the semi-parametric model, the test statistic used in the paper for for testing $H_0$ is:
$$ I = \left[X^T\tilde{\beta}+Z^T\tilde{\gamma}- X^T\hat{\beta}-\hat{\theta}(Z)\right]^2 $$
Under $H_0$, $I$ converges to 0 in probability, while it converges to a positive constant under $H_1$. Therefore, the statistic $I$ can be used to detect whether $H_0$ is true or not. However, given some problems with the asymptotical distribution of $I$, the authors propose to compute its empirical distribution by resampling $u$, the residuals, $n$ times, using those residuals to generate $n$ new $Y$s and then re-estimating both models $n$ times. By this way it is possible to obtain $n$ estimates of $I^*$ and its empirical distribution which should be approximating the null distribution of $I$. Therefore it can be used to detect whether $H_0$ holds.
My problem is in the interpretation of the results of the test. I reasoned as follows: I plotted the empirical distribution of $I^*$ which, in my case, has mean > 0. Therefore what I did was to verify where the $I$ statistic lies. This is what I obtain:
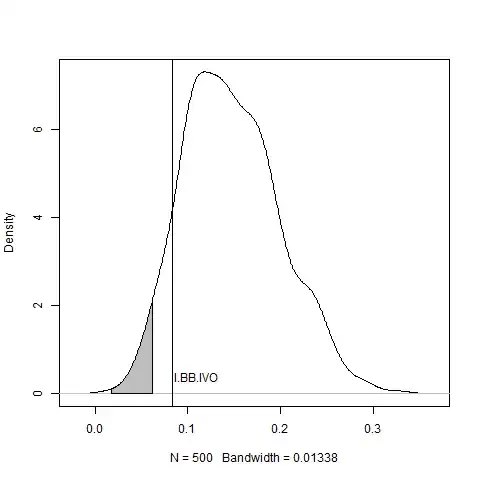
where I.BB.IVO is my $I$. Can I say that $I$ belongs to the empirical distribution (since it is not in the rejection zone) with mean > 0, therefore the null hypothesis is rejected?
Is there any other alternative of doing the job?