45

I am new to statistics and I currently deal with ANOVA. I carry out an ANOVA test in R using

aov(dependendVar ~ IndependendVar)

I get – among others – an F-value and a p-value.

My null hypothesis ($H_0$) is that all group means are equal.

There is a lot of information available on how F is calculated, but I don't know how to read an F-statistic and how F and p are connected.

So, my questions are:

  1. How do I determine the critical F-value for rejecting $H_0$?
  2. Does each F have a corresponding p-value, so they both mean basically the same? (e.g., if $p<0.05$, then $H_0$ is rejected)
chl
  • 50,972
  • 18
  • 205
  • 364
JanD
  • 561
  • 1
  • 5
  • 6
  • 1
    Have you tried the commands `summary(aov(dependendVar ~ IndependendVar)))` or `summary(lm(dependendVar ~ IndependendVar))`? Do you mean all the group means are equal to each other and equal to 0 or just to each other? – HazelnutCoffee Jun 27 '11 at 15:46
  • yes, I did try the `summary(aov...)`. Thanks for the `lm.*`, did not know about this :-) I don't get what you mean by equal to 0. If that's short for my 0-Hypothesis than the Hypothesis would need a value, and I did not test on specific one, so in this case: just to each other! – JanD Jun 27 '11 at 19:57
  • 1
    For an intuitive explanation look at the [Yhat](http://blog.yhat.com/posts/r-lm-summary.html) blog on the topic of regression. – DataTx Mar 22 '16 at 05:55

3 Answers3

33

The F statistic is a ratio of 2 different measure of variance for the data. If the null hypothesis is true then these are both estimates of the same thing and the ratio will be around 1.

The numerator is computed by measuring the variance of the means and if the true means of the groups are identical then this is a function of the overall variance of the data. But if the null hypothesis is false and the means are not all equal, then this measure of variance will be larger.

The denominator is an average of the sample variances for each group, which is an estimate of the overall population variance (assuming all groups have equal variances).

So when the null of all means equal is true then the 2 measures (with some extra terms for degrees of freedom) will be similar and the ratio will be close to 1. If the null is false, then the numerator will be large relative to the denominator and the ratio will be greater than 1. Looking up this ratio on the F-table (or computing it with a function like pf in R) will give the p-value.

If you would rather use a rejection region than a p-value, then you can use the F table or the qf function in R (or other software). The F distribution has 2 types of degrees of freedom. The numerator degrees of freedom are based on the number of groups that you are comparing (for 1-way it is the number of groups minus 1) and the denominator degrees of freedom are based on the number of observations within the groups (for 1-way it is the number of observations minus the number of groups). For more complicated models the degrees of freedom get more complicated, but follow similar ideas.

Greg Snow
  • 46,563
  • 2
  • 90
  • 159
  • Thanks for the explanation! I assume that if I can look up the F value on a table to see the p-value, than the the p and F are just two ways to express the likelyhood that a result like the one analysed can occur if the H0 is right? – JanD Jun 27 '11 at 19:49
  • 2
    In all parametric statistics there is a direct functional link between the test statistic (F in this case) and the p-value. These have been put into table for convenience, but can also be computed directly. You can either use alpha to find the cut-off for a critical region to compare the test statistic to (which I think is more intuitive) or use the computed test statistic to find the p-value to compare to alpha. In either case we start with an alpha level and a test statistic formula that follows a given distribution when the null is true. – Greg Snow Jun 28 '11 at 18:00
22

The best way to think about the relationship between $F$, $p$, and the critical value is with a picture:

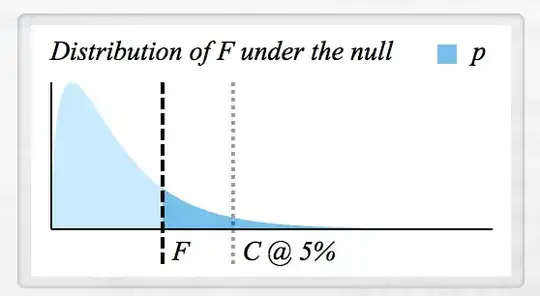
enter image description here

The curve here is an $F$ distribution, that is, the distribution of $F$ statistics that we'd see if the null hypothesis were true. In this diagram, the observed $F$ statistic is the distance from black dashed line to the vertical axis. The $p$ value is the dark blue area under the curve from $F$ to infinity. Notice that every value of $F$ must correspond to a unique $p$ value, and that higher $F$ values correspond to lower $p$ values.

You should notice a couple of other things about the distribution under null hypothesis:

1) $F$ values approaching zero are highly unlikely (this is not always true, but it's true for the curve in this example)

2) After a certain point, the larger the $F$ is, the less likely it is. (The curve tapers off to the right.)

The critical value $C$ also makes an appearance in this diagram. The area under the curve from $C$ to infinity equals the significance level (here, 5%). You can tell that the $F$ statistic here would result in a failure to reject the null hypothesis because it is less than $C$, that is, its $p$ value is greater than .05. In this specific example, $p=0.175$, but you'd need a ruler to calculate that by hand :-)

Note that the shape of the $F$ distribution is contingent on its degrees of freedom, which for ANOVA correspond to the # of groups (minus 1) and # of observations (minus the # of groups). In general, the overall "shape" of the $F$ curve is determined by the first number, and its "flatness" is determined by the second number. The above example has a $df_1 = 3$ (4 groups), but you'll see that setting $df_1 = 2$ (3 groups) results in a markedly different curve:

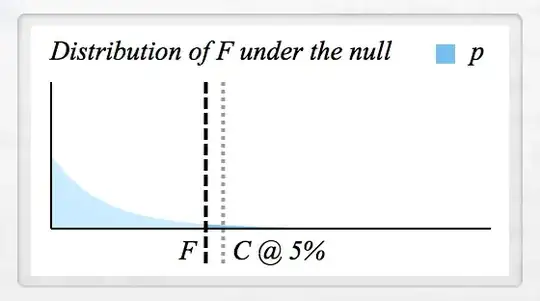
enter image description here

You can see other variants of the curve on Mr. Wikipedia Page. One thing worth noting is that because the $F$ statistic is a ratio, large numbers are uncommon under the null hypothesis, even with large degrees of freedom. This is in contrast to $\chi^2$ statistics, which are not divided by the number of groups, and essentially grow with the degrees of freedom. (Otherwise $\chi^2$ is analogous to $F$ in the sense that $\chi^2$ is derived from normally distributed $z$ scores, whereas $F$ is derived from $t$-distributed $t$ statistics.)

That's a lot more than I meant to type, but I hope that covers your questions!

(If you're wondering where the diagrams came from, they were automatically generated by my desktop statistics package, Wizard.)

Emiller
  • 471
  • 3
  • 5
14

To answer your questions:

  1. You find the critical F value from an F distribution (here's a table). See an example. You have to be careful about one-way versus two-way, degrees of freedom of numerator and denominator.

  2. Yes.

dfrankow
  • 2,816
  • 6
  • 30
  • 39
  • It is not meaningful to talk about one- or two-way comparisons in an omnibus test such as the F-test. – Marcus Morrisey Apr 16 '14 at 20:19
  • 4
    Marcus Morrisey: I think you're confusing one vs two tails with one- vs two-way. The F-test doesn't have multiple "tails" to choose from, but one-way ANOVA vs two-way ANOVA needs to be considered when constructing the test statistic. – Emiller Oct 09 '14 at 20:01